Câu hỏi:
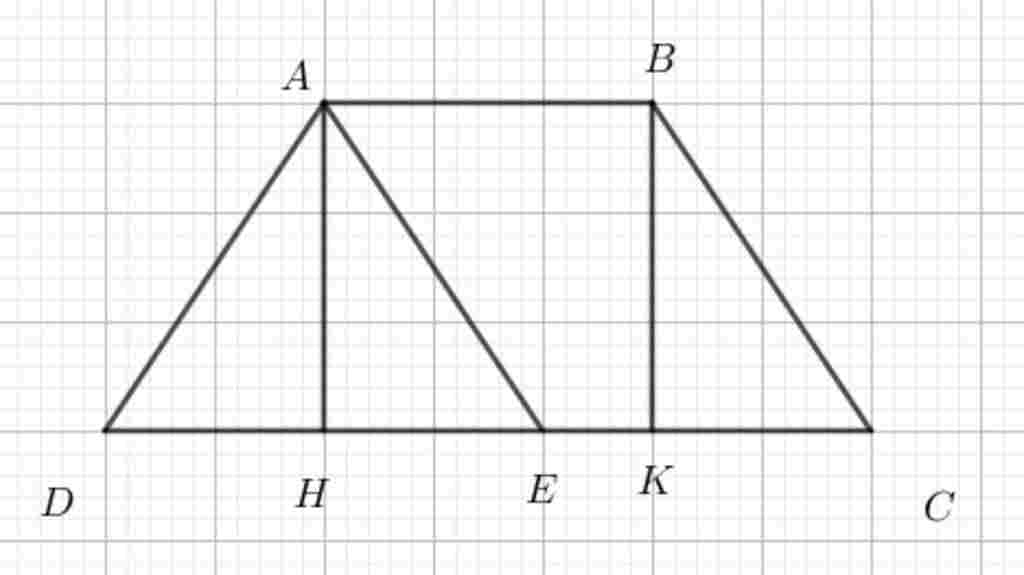
Giúp em bài tập về nhà Toán lớp 8 câu hỏi như sau: Cho hình thang cân: ABCD (AB//CD ). Các đường AH, BK
a) tứ giác ANKH là hình gì? Tại sao
b) DH=CK
c) gọi E là điểm đối xứng của D qua H. Hỏi D và E đối xứng với E qua đường nào
d) tứ giác ADCE là hình gì
Trả lời 2:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
Giải đáp:
Lời giải và giải thích chi tiết:
Giải:
a)Xét tứ giác ABKH có: AB//HK,AH//BK(cùng vuông góc với CD)
=>ABKH là hình bình hành
Kết hợp có 1 góc vuông
=>ABKH là hình chữ nhật
b)Xét tam giác ADH và tam giác BCK có:
AH=BK,AD=BC,góc AHD=góc BKC=90^0
=>Tam giác ADH=tam giác BCK
=>DH=CK(dpcm)
c)Do E là điểm đối xứng của D qua H nên:
góc AED=góc ADH=góc BCK
=>AE//BC
Kết hợp AB//EC
=>ABCE là hình bình hành
d)DH+CK=CD-HK=CD-AB
=>DH=(CD-AB)/2(Do: DH=CK)
Trả lời 1:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
a) Tứ giác $ABKH$ có $AB\parallel HK, AH\parallel BK$ (cùng $\bot DC$)
$\Rightarrow ABKH$ là hình bình hành có $\widehat H=90^o$
$\Rightarrow ABKH$ là hình chữ nhật.
b) Tứ giác $ABKH$ là hình chữ nhật $\Rightarrow AH=BK$
Xét $\Delta$ vuông $ AHD$ và $\Delta$ vuông $ BKC$ có:
$AH=BK$
$AD=BC$
$\Rightarrow\Delta $ vuông $AHD=\Delta $ vuông $BKC$ (2 cạnh góc vuông)
$\Rightarrow DH=CK$ (2 cạnh tương ứng )
c) E đối xứng với D qua H, do đó H là trung điểm của ED
Lại có $AH\bot ED$
Nên $D,E $ đối xứng với nhau qua đường $AH$
d) Xét $\Delta$ vuông $AHD$ và $\Delta AHE$ có:
$AH$ chung
$DH=HE$
$\Rightarrow \Delta$ vuông $AHD=\Delta AHE$ (2 cạnh góc vuông)
$\widehat{AEH}=\widehat{ADH}$ (2 góc tương ứng)
mà $\widehat{ADH}=\widehat{BCK}$
$\Rightarrow \widehat{AEH}=\widehat{BCK}$ mà chúng ở vị trí đồng vị
$\Rightarrow AE\parallel BC$ lại có $AB\parallel EC$
$\Rightarrow ABCE$ là hình bình hành.