Câu hỏi:
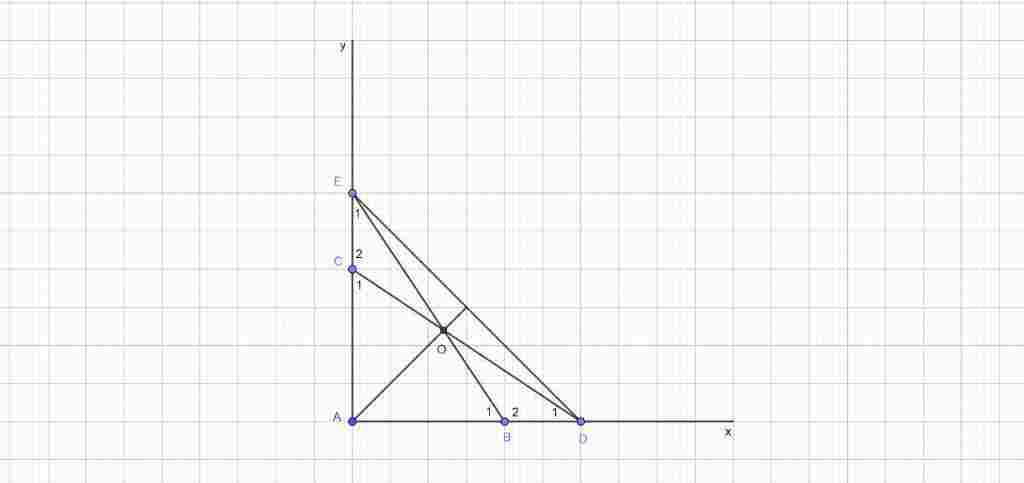
Giúp em bài tập về nhà Toán lớp 7 câu hỏi như sau: cho góc vuông xAy, trên tia Ax lấy 2 điểm B&D, trên tia Ay lấy 2 điểm C&E sao cho AB=AC, AD=AE
a) chứng minh tam giác ACD và tam giác ABE bằng nhau
b) chứng minh tam giác BOD và COE bằng nhau. Với O là giao điểm của DC,BE
c) chứng minh AO vuông góc với DE
Trả lời 2:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
a) Xét ΔACD và ΔABE, ta có:
c: AB = AC (giả thiết)
c: AE = AD (giả thiết)
g: góc A = 90 độ hoặc góc A là góc chung ⇔ Chọn 1 trong 2 ( giả thiết)
⇒ ΔACD = ΔABE ( c-g-c)
b) CO = OB
DO = EO
=> CO + DO = OB + EO
=> CD = EB
Xét ΔBOD và ΔABE, ta có:
c: CO = OB ( chứng minh trên)
c: DO = EO ( chứng minh trên)
g: góc EOC = góc BOD ( giả thiết)
=> ΔBOD = ΔABE (c-g-c)
c) ΔACD = ΔABE ( chứng minh trên)
=> góc AOC + góc AOB = 180 độ (2 góc kề bù)
Mà góc AOC = góc AOB = 180 độ : 2 = 90 độ
Vậy AO⊥BE ( chỉnh đề một chút)
” Nếu chỉnh đề sai, mong bạn sửa lại và làm giống cách trên
Chúc bạn học tốt
Trả lời 1:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
a/ Xét $\Delta{ACD}$ và $\Delta{ABE}$:
$AB=AC(gt)$
$\widehat{A}:chung$
$AD=AE(gt)$
$\to \Delta{ACD}=\Delta{ABE}(c-g-c)$
b/ $\Delta{ACD}=\Delta{ABE}$
$\to \widehat{B_1}=\widehat{C_1}$ (2 góc tương ứng)
mà $\begin{cases}\widehat{B_1}+\widehat{B_2}=180^o\\\widehat{C_1}+\widehat{C_2}=180^o\end{cases}$
$\to \widehat{B_2}=\widehat{C_2}$
$AD=AE$ mà $AB=AC$
$\to AD-AB=AE-AC$ hay $CE=BD$
Xét $\Delta{BOD}$ và $\Delta{COE}$:
$\widehat{B_2}=\widehat{C_2}(cmt)$
$CE=BD(cmt)$
$\widehat{E_1}=\widehat{D_1}$ ($\Delta{ACD}=\Delta{ABE}$)
$\to \Delta{BOD}=\Delta{COE}(g-c-g)$
c/ $\Delta{BOD}=\Delta{COE}$
$\to BO=CO$ (2 cạnh tương ứng)
Xét $\Delta{ABO}$ và $\Delta{ACO}$:
$BO=CO(cmt)$
$\widehat{B_1}=\widehat{C_1}(cmt)$
$AB=AC(gt)$
$\to \Delta{ABO}=\Delta{ACO}(c-g-c)$
$\to \widehat{BAO}=\widehat{CAO}$ (2 góc tương ứng)
$\to AO$ là đường phân giác $\widehat{A}$
mà $\Delta{ADE}$ cân tại $A$ ($AD=AE$)
$\to AO$ là đường cao $DE$
$\to AO\perp DE$