Câu hỏi:
Giúp em bài tập về nhà Vật lý lớp 9 câu hỏi như sau: Chứng MInh
Ảnh thật : 1/f = 1/d + 1/d’
Thấu kính hội tụ :
Ảnh ảo : 1/f = 1d – 1d’
TKPK : 1/f = 1d’ – 1/d
Trả lời 1:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
XÉT VỚI THẤU KÍNH HỘI TỤ:
Hình L1 (ảnh thật)
Ta có:
+ \(\Delta OAB\~\Delta OA’B’\)
\( \Rightarrow \dfrac{{AB}}{{A’B’}} = \dfrac{{OA}}{{OA’}}\) (1)
+ \(\Delta F’IO\~\Delta F’B’A’\)
\( \Rightarrow \dfrac{{I{\rm{O}}}}{{A’B’}} = \dfrac{{F’O}}{{F’A’}}\) (2)
Mà \(IO=AB\)
Từ (1) và (2) ta suy ra:
\(\begin{array}{l}\dfrac{{OA}}{{OA’}} = \dfrac{{F’O}}{{F’A’}} \Leftrightarrow \dfrac{{OA}}{{OA’}} = \dfrac{{F’O}}{{OA’ – F’O}}\\ \Leftrightarrow \dfrac{{OA’}}{{OA}} = \dfrac{{OA’ – F’O}}{{F’O}} = \dfrac{{OA’}}{{F’O}} – 1\\ \Rightarrow \dfrac{{OA’}}{{OA}} = \dfrac{{OA’}}{{F’O}} – \dfrac{{OA’}}{{OA’}}\\ \Rightarrow \dfrac{1}{{OA}} = \dfrac{1}{{F’O}} – \dfrac{1}{{OA’}}\\ \Rightarrow \dfrac{1}{{F’O}} = \dfrac{1}{{OA}} + \dfrac{1}{{OA’}}\end{array}\)
Hay \(\dfrac{1}{f} = \dfrac{1}{d} + \dfrac{1}{{d’}}\) (ĐPCM)
Hình L2 (ảnh ảo)
+ $\Delta OAB\~\Delta OA’B’ \Rightarrow \dfrac{{AB}}{{A’B’}} = \dfrac{{OA}}{{OA’}}\left( 1 \right)$
+ \(\Delta F’OI\~\Delta F’A’B’ \Rightarrow \dfrac{{OF’}}{{A’F’}} = \dfrac{{OI}}{{A’B’}}\left( 2 \right)\)
Lại có: \(OI = AB\)
\(\begin{array}{l} \Rightarrow \dfrac{{OA}}{{OA’}} = \dfrac{{{\rm{OF}}’}}{{AF’}} \Rightarrow \dfrac{{OA’}}{{OA}} = \dfrac{{AF’}}{{OF’}} = \dfrac{{OA’ + {\rm{OF}}’}}{{{\rm{OF}}’}} = \dfrac{{OA’}}{{{\rm{OF}}’}} + 1\\ \Leftrightarrow \dfrac{{OA’}}{{OA}} = \dfrac{{OA’}}{{OF’}} + \dfrac{{OA’}}{{OA’}}\\ \Rightarrow \dfrac{1}{{OA}} = \dfrac{1}{{OF’}} + \dfrac{1}{{OA’}}\\ \Rightarrow \dfrac{1}{{OF’}} = \dfrac{1}{{OA}} – \dfrac{1}{{OA’}}\end{array}\)
Hay \(\dfrac{1}{f} = \dfrac{1}{d} – \dfrac{1}{{d’}}\) (ĐPCM)
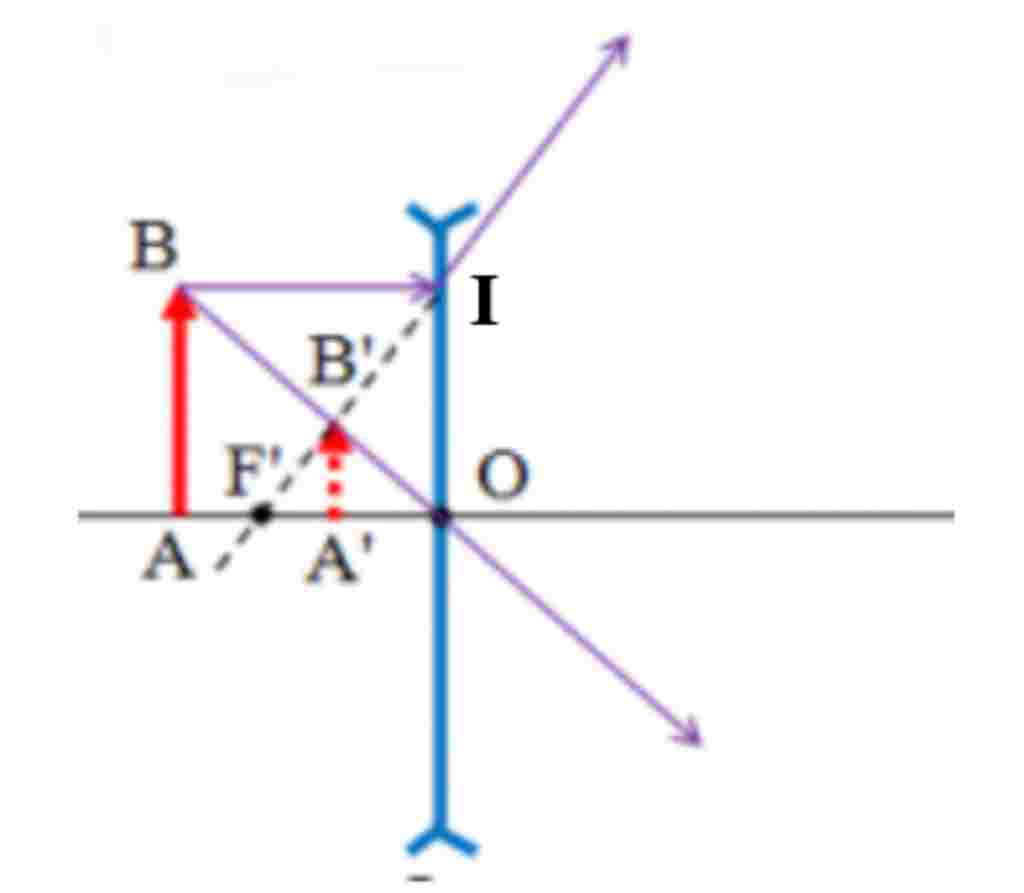
XÉT VỚI THẤU KÍNH PHÂN KÌ
Ta có:
+ \(\Delta OAB\~\Delta OA’B’ \Rightarrow \dfrac{{AB}}{{A’B’}} = \dfrac{{OA}}{{OA’}}\left( 1 \right)\)
+ \(\Delta I{\rm{OF’\~}}\Delta {\rm{B’A’F’}} \Rightarrow \dfrac{{IO}}{{B’A’}} = \dfrac{{{\rm{O}}F’}}{{A’F’}}\left( 2 \right)\)
Mà \(IO = AB\)
Từ (1) và (2) ta suy ra:
\(\begin{array}{l}\dfrac{{OA}}{{OA’}} = \dfrac{{O{\rm{F’}}}}{{A’F’}}\\ \Rightarrow \dfrac{{OA’}}{{OA}} = \dfrac{{A’F’}}{{{\rm{OF}}’}} = \dfrac{{{\rm{OF}}’ – OA’}}{{OF’}} = 1 – \dfrac{{OA’}}{{OF’}}\\ \Leftrightarrow \dfrac{{OA’}}{{OA}} = \dfrac{{OA’}}{{OA’}} – \dfrac{{OA’}}{{OF’}}\\ \Rightarrow \dfrac{1}{{OA}} = \dfrac{1}{{OA’}} – \dfrac{1}{{OF’}}\\ \Rightarrow \dfrac{1}{{OF’}} = \dfrac{1}{{OA’}} – \dfrac{1}{{OA}}\end{array}\)
Hay \(\dfrac{1}{f} = \dfrac{1}{{d’}} – \dfrac{1}{d}\) (ĐPCM)