Câu hỏi:
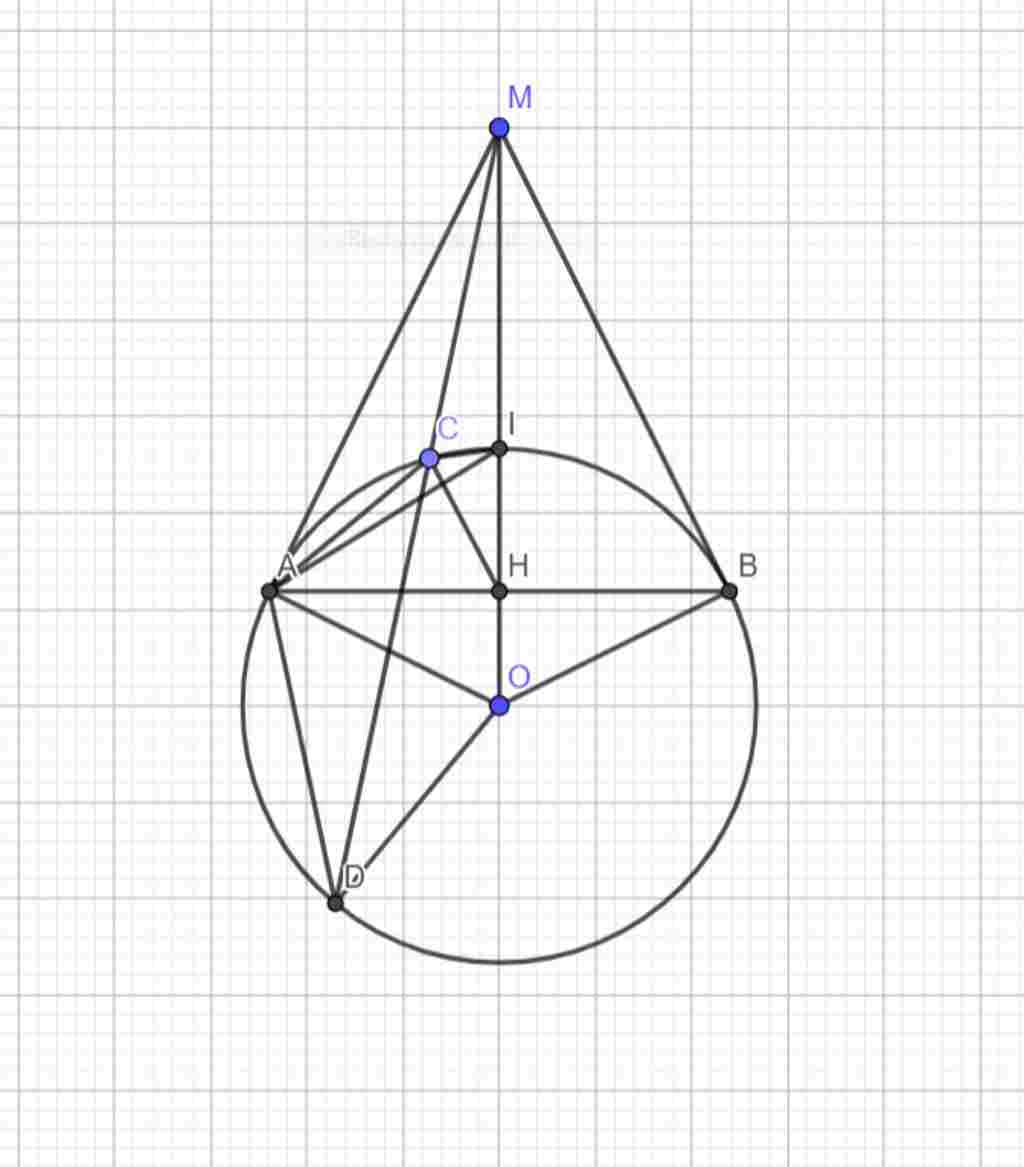
Giúp em bài tập về nhà Toán lớp 9 câu hỏi như sau: cho điểm M nằm ngoài đường tròn (O). vẽ tiếp tuyến MA,MB với đường tròn (O) với A và B là các tiếp điểm. vẽ cát tuyến MCD không đi qua tâm O ( C nằm giữa M và D), OM cắt AB với đường tròn (O) lần lượt tại H và I. chứng minh
1, tứ giác MAOB nội tiếp
2, MC.MD=MA2
3, OH.+MC.MD=MO2
4, CI là tia phân giác góc MCH
Trả lời 2:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
1, *Xét tứ giác MAOB có :
góc MAO = 90∘ (vì MA là tiếp tuyến của đường tròn )
góc MBO = 90∘ (vì MB là tiếp tuyến của đường tròn )
⇒ góc MAO + góc MBO = 90∘+90∘ = 180∘ (2 góc đối nhau)
⇒ tứ giác MAOB nội tiếp (d/h)
2, *Xét ΔMAC và ΔMDA có :
góc MAC = góc MDA (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung AC)
góc AMD chung
⇒ ΔMAC ∝ ΔMDA (g.g)
⇒$\frac{MA}{MD }$ = $\frac{MC}{MA}$ (c.c.t.ư)
⇒MA^2 = MC.MD(đpcm)
3, * Có : MA =MB (t/c 2 tiếp tuyến cắt nhau) ⇒ Điểm M cách đều 2 điểm A,B
OA = OB = R ⇒ Điểm O cách đều 2 điểm A,B
Suy ra OM là đường trung trực của AB (t/c)
⇒ OM ↓ AB tại H
⇒ AH là đường cao
* Xét ΔMAO có góc MAO = 90∘(cmt) , đường cao AH (cmt)
⇒ MH.MO = MA² (hệ thức lượng trong Δ vuông)
⇒ OH.OM=OA²( hệ thức lượng trong Δ vuông ) (1)
* có : MC.MD=MA² (cmt) (2)
* Cộng vế với vế (1),(2) ta được :
OH.OM+MC.MD = OA² + MA² = MO²(đpcm) (OA²+MA²=OM² theo pitago)
4, * Có : MH.MO = MA²(cmt)
MC.MD=MA² (cmt)
⇒ MH.MO=MC.MD
⇒$\frac{MC}{MH}$ = $\frac{MO}{MD}$
*Xét Δ MCH và ΔMOD có :
$\frac{MC}{MH}$ = $\frac{MO}{MD}$ (cmt)
góc DMO chung
⇒ Δ MCH ∝ ΔMOD (c.g.c)
⇒ góc MHC = góc MDO(c.g.t.u)
* Xét tứ giác CHOD có : góc MHC = góc MDO(cmt)
⇒ tứ giác CHOD nội tiếp (d/h)
⇒ góc HCD = góc KOD (t/c)
* Có : góc KCD = $\frac{1}{2}$ sđ cung DK (góc ntiếp chắn cung DK)
góc KOD = sđ cung DK (góc ở tâm chắn cung DK)
⇒góc KCD = $\frac{1}{2}$ góc KOD = $\frac{1}{2}$ góc HCD(vì góc HCD = góc KOD cmt )
⇒ CK là tia p/g của góc HCD (t/c) (3)
*Mà góc ICK = 90∘(góc ntiếp chắn nửa đường tròn)
⇒ IC ↓ CK (4)
Từ (3) , (4) suy ra : CI là tia phân giác góc MCH (đpcm)
Trả lời 1:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
Lời giải và giải thích chi tiết:
1.Vì $MA,MB$ là tiếp tuyến của (O)
$\to MA\perp OA,MB\perp OB$
$\to MAOB$ nội tiếp đường tròn đường kinh $MO$
2.Vì $MA$ là tiếp tuyến của (O)
$\to\widehat{MAC}=\widehat{MDA}$
$\to\Delta MAC\sim\Delta MDA(g.g)$
$\to\dfrac{MA}{MD}=\dfrac{MC}{MA}$
$\to MA^2=MC.MD$
3.Vì $MA,MB$ là tiếp tuyến của (O)
$\to MO\perp AB=H$
$\to AH\perp MO$
Mà $MA\perp OA\to MA^2=MH.MO$
$\to MC.MD=MH.MO$
$\to OH.OM+MC.MD=OH.OM+MH.MO=OM(OH+MH)=OM^2$
d.Ta có $MA,MB$ là tiếp tuyến của (O)
$\to MO$ là trung trực của $AB\to IA=IB$
$\to\widehat{MAI}=\widehat{IBA}=\widehat{IAB}$
$\to AI$ là phân giác $\widehat{MAH}$
$\to \dfrac{IH}{IM}=\dfrac{AH}{AM}$
Ta có $\widehat{MHA}=\widehat{MAO}=90^o$
$\to\Delta MAH\sim\Delta MOA(g.g)$
$\to\dfrac{AH}{AO}=\dfrac{MA}{MO}$
$\to \dfrac{AH}{AM}=\dfrac{OA}{MO}$
Từ câu 3 ta có : $MC.MD=MH.MO$
$\to \dfrac{MC}{MH}=\dfrac{MO}{MD}$
$\to\Delta MCH\sim\Delta MOD(c.g.c)$
$\to \dfrac{MC}{MO}=\dfrac{CH}{OD}$
$\to \dfrac{MC}{CH}=\dfrac{MO}{OD}=\dfrac{MO}{OA}$ vì $OA=OD=R$
$\to \dfrac{CH}{MC}=\dfrac{OA}{OM}=\dfrac{AH}{AM}=\dfrac{IH}{IM}$
$\to CI$ là phân giác $\widehat{MCH}$