Câu hỏi:
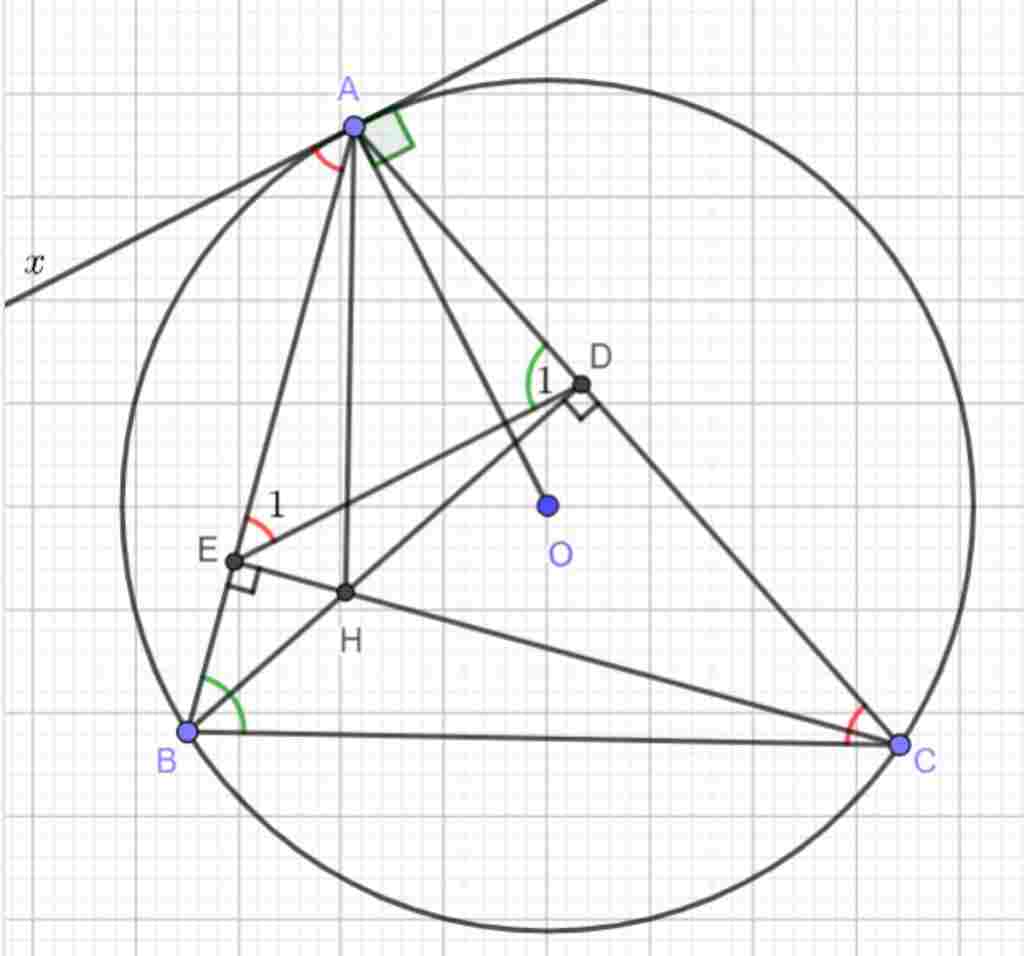
Giúp em bài tập về nhà Toán lớp 9 câu hỏi như sau: Cho tam giác nhọn ABC nội tiếp đường tròn O , các đường cao BD và CE cắt nhau tại H
a. Chứng minh rằng các tứ giác ADHE và BDEC nội tiếp
b. Chứng minh rằng AE.AB= AD.AC
c. Chứng minh rằng OA vuông góc với DE
Trả lời 1:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
a) Xét tứ giác $ADHE$ có:
$\widehat{AEH}=90^o$ (do $CE\bot AB$)
$\widehat{ADH}=90^o$ (do $BD\bot AC$)
$\Rightarrow\widehat{AEH}+\widehat{ADH}=180^o$
$\Rightarrow ADHE$ nội tiếp đường tròn đường kính $(AH)$
Xét tứ giác $BEDC$ có:
$\widehat{BEC}=90^o$ (do $CE\bot AB$)
$\widehat{BDC}=90^o$ (do $BD\bot AC$)
Hai đỉnh E, D cùng nhìn BC dưới một góc $90^o$
$\Rightarrow $ tứ giác $BEDC$ nội tiếp đường tròn đường kính $(BC)$
b) Do tứ giác $BEDC$ nội tiếp nên $\widehat{D_1}=\widehat B$ (tính chất tứ giác nội tiếp)
Xét $\Delta AED$ và $\Delta ACB$ có:
$\widehat A$ chung
$\widehat {D_1}=\widehat B$ (cmt)
$\Rightarrow\Delta AED\sim\Delta ACB$ (g.g)
$\Rightarrow\dfrac{AE}{AC}=\dfrac{AD}{AB}$
$\Rightarrow AE.AB=AD.AC$ (đpcm)
c) Gọi $Ax$ là tiếp tuyến của $(O)$ tại $A$
Ta có tứ giac $BEDC$ nội tiếp đường tròn đường kính $(BC)$ nên $\widehat{E_1}=\widehat {DCB}$ (tc)
$\widehat{BAx}=\widehat{DCB}$ (góc tạo bởi tiếp tuyến, dây cung và góc nội tiếp cùng chắn cung AB)
Từ hai điều trên suy ra $\widehat{E_1}=\widehat{BAx}$ mà chúng ở vị trí so le trong
$\Rightarrow Ax//ED$ và có $OA\bot Ax$ (cách dựng)
$\Rightarrow OA\bot ED$ (từ vuông góc đến song song).