Câu hỏi:
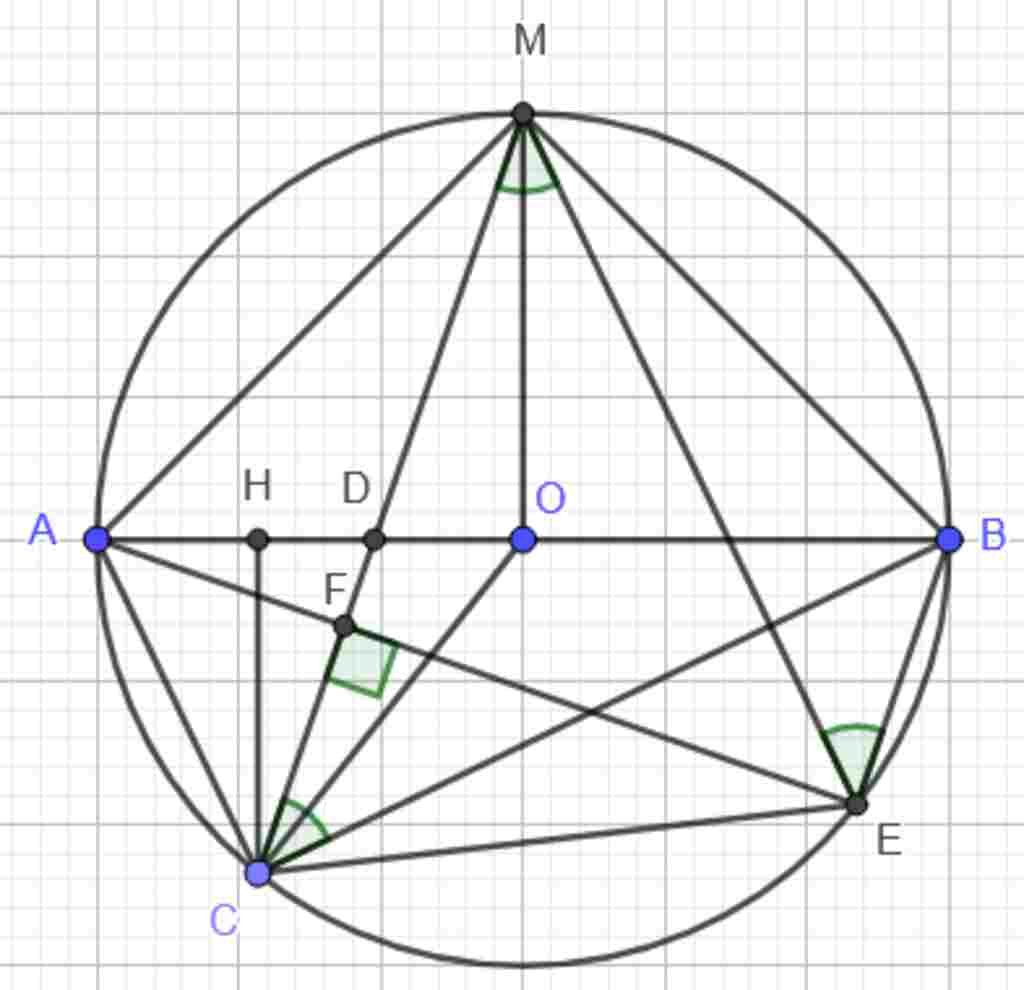
Giúp em bài tập về nhà Toán lớp 9 câu hỏi như sau: Cho đường tròn (O) đường kính AB. M là điểm chính giữa của một nửa đường tròn, C là điểm bất kì trên nửa đường tròn kia, CM cắt AB tại D. Vẽ dây AE vuông CM tại F
a) Chứng minh ACEM là hình thang cân.
b) Vẽ CH vuông góc AB, chứng minh CN là tia phân giác của góc HCO.
Giúp mình với mình siêu gấp luôn ạ huhuhuhu
Trả lời 2:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
Giải đáp:
Lời giải và giải thích chi tiết:\
AECM là hình thang cân => AE=CM
CD<hoặc bằng 1/2 AE
<=> C với M qua O
cung KB=CA cung
cung AC=AT cung
cung KB=AT cung
=> điều phải chứng minh
Thực chất 2 câu này dễ mà trong sách có giải hơi sơ sài
=> Điều phải chứng minh
M ở chính giữa => AM = 90độ
Góc nội típ=1/2
Trả lời 1:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
a) $\widehat{AEB}=90^o$ (góc nội tiếp chắn nửa đường tròn) $\Rightarrow BE\bot AE$ mà $CM\bot AE$ (giả thiết)
$\Rightarrow BE\parallel CM\Rightarrow \widehat{CME}=\widehat{MEB}$ (hai góc ở vị trí so le trong)
Mà $\widehat{MCB}=\widehat{MEB}$ (góc nội tiếp cùng chắn cung MB)
$\Rightarrow \widehat{CME}=\widehat{MCB}$ $(=\widehat{MEB})$
$\Rightarrow $ cung CE = cung MB
mà cung MB=cung AM (do M là điểm chính giữa của cung AB)
$\Rightarrow$ cung $AM=$ cung $CE\Rightarrow AM=CE$ (1) và
$\widehat{ACM}=\widehat{CME}$ (góc nội tiếp cùng chắn 2 cung bằng nhau cung AM=cung CE) mà chúng ở vị trí so le trong nên $AC//ME\Rightarrow ACEM$ là hình thang lại có thêm AM=CE (cmt) $\Rightarrow ACEM$ là hình thang cân
b) Do M là điểm chính giữa của cung AB nên $MO\bot AB$
$CH\bot AB$ (giả thiết)
$\Rightarrow MO//CH\Rightarrow \widehat{HCM}=\widehat{CMO}$ (hai góc ở vị trí so le trong) (2)
$\Delta OCM$ cân đỉnh O (OM=OC=R) $\Rightarrow \widehat{MCO}=\widehat{CMO}$ (3)
Từ (2) và (3) suy ra $\widehat{HCM}=\widehat{MCO}$
$\Rightarrow CM$ là phân giác của $\widehat{HCO}$ (đpcm)