Câu hỏi:
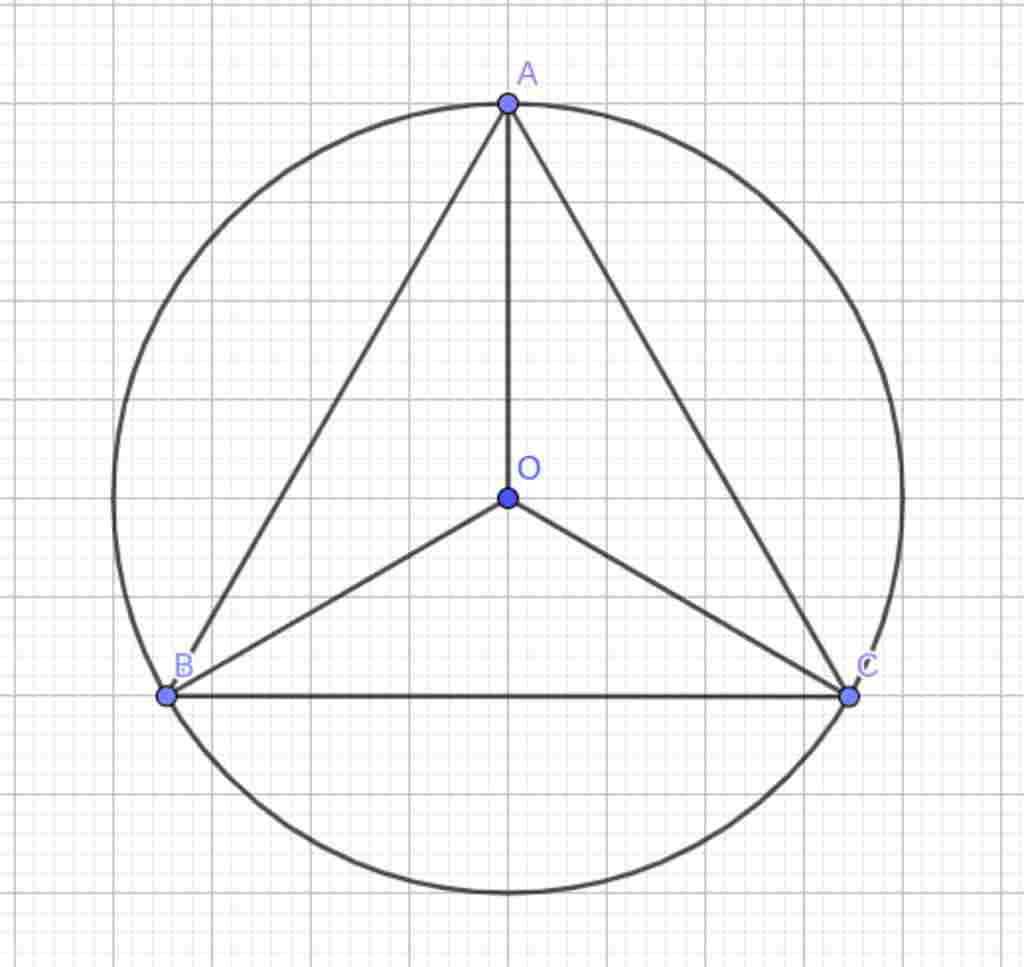
Giúp em bài tập về nhà Toán lớp 9 câu hỏi như sau: Cho tam giác ABC đều nội tiếp đường tròn (o).
a, Tính số đo cung ACnhỏ, cung AClớn
b, Tính số đo góc ở tâm: góc AOB, góc BOC. Tính góc OAC.
Trả lời 1:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
Lời giải và giải thích chi tiết:
a.Vì $\Delta ABC$ đều $\rightarrow O$ vừa là trọng tâm, trực tâm, tâm đường tròn nội tiếp $\Delta ABC$
$\rightarrow \widehat{AOC}=2\widehat{ABC}=120^o$
$\rightarrow \text{Số đo cung }AC_{nhỏ}=120^o$
$\rightarrow \text{Số đo cung }AC_{lớn}}=360^o-120^o=240^o$
b.Tương tự
$\rightarrow \widehat{AOB}=\widehat{BOC}=120^o$
$\widehat{OAC}=\widehat{OCA}=\dfrac{1}{2}(180^o-\widehat{AOC})=30^o$