Câu hỏi:
Giúp em bài tập về nhà Toán lớp 9 câu hỏi như sau: Tính diện tích hình quạt tròn OAmB theo R biết O của hình tròn có bán kỉnh, dây AB=R căn3
Trả lời 2:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
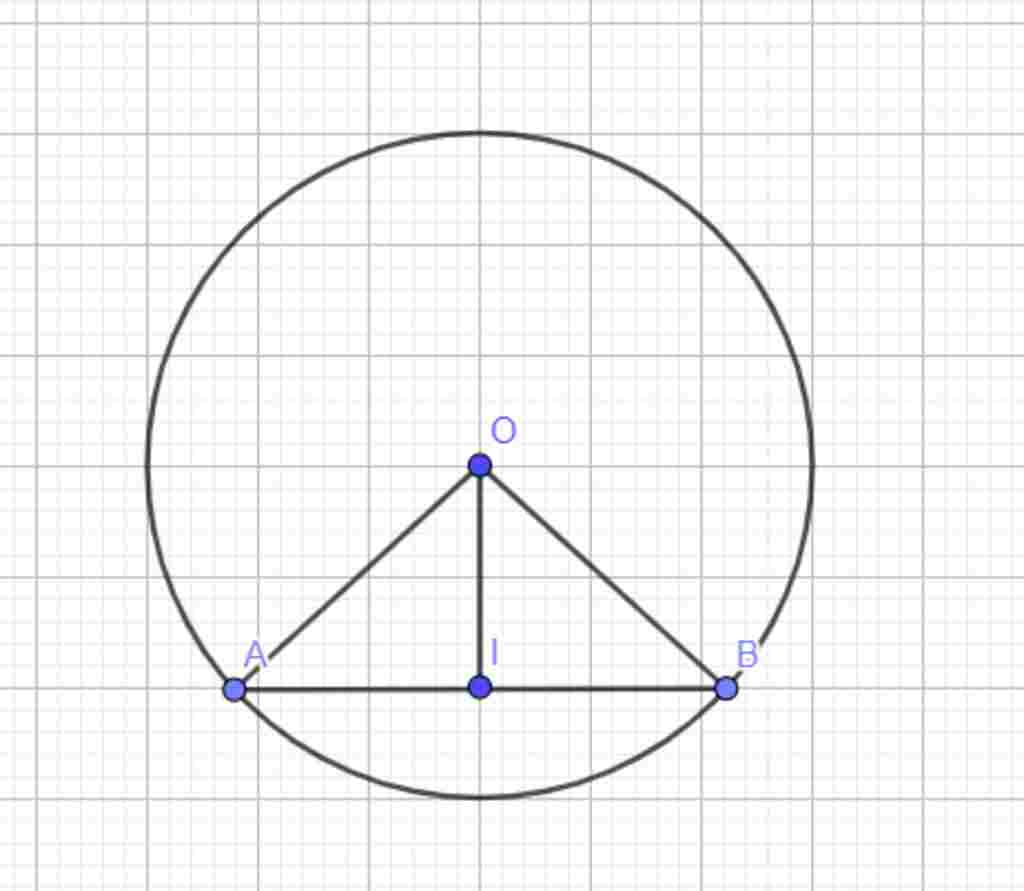
Bạn xem hình

Trả lời 1:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
Giải đáp:
${S_{}} = \dfrac{{\pi {R^2}}}{3}$
Lời giải và giải thích chi tiết:
Ta có:
${S_{}} = \dfrac{{\pi {R^2}sd\widehat {AOB}}}{{360}} = \dfrac{{\pi {R^2}.2sd\widehat {AOI}}}{{360}}$
Gọi $I$ là trung điểm của $AB$
Theo tính chất của đường tròn $\to OI\bot AB=I$
Lại có:
$\begin{array}{l}
\Delta AOI;\widehat {AIO} = {90^0};AO = R;AI = \dfrac{{AB}}{2} = \dfrac{{R\sqrt 3 }}{2}\\
\Rightarrow \sin \widehat {AOI} = \dfrac{{AI}}{{AO}} = \dfrac{{\sqrt 3 }}{2}\\
\Rightarrow \widehat {AOI} = {60^0}\\
\Rightarrow {S_{}} = \dfrac{{\pi {R^2}.2sd\widehat {AOI}}}{{360}} = \dfrac{{\pi {R^2}.2.60}}{{360}} = \dfrac{{\pi {R^2}}}{3}
\end{array}$
Vậy ${S_{}} = \dfrac{{\pi {R^2}}}{3}$