Câu hỏi:
Giúp em bài tập về nhà Toán lớp 9 câu hỏi như sau: Cho phương trình : 2x^2-3x-7=0
A) Chứng minh phương trình có 2 nghiệm phân biệt x1,x2
B) Không giải phương trình tính tổng và tích 2 nghiệm
C) Không giải phương trình tính
x1-1/x2 + x2-1/x1
Trả lời 2:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
Đáp án:
Giải thích các bước giải:
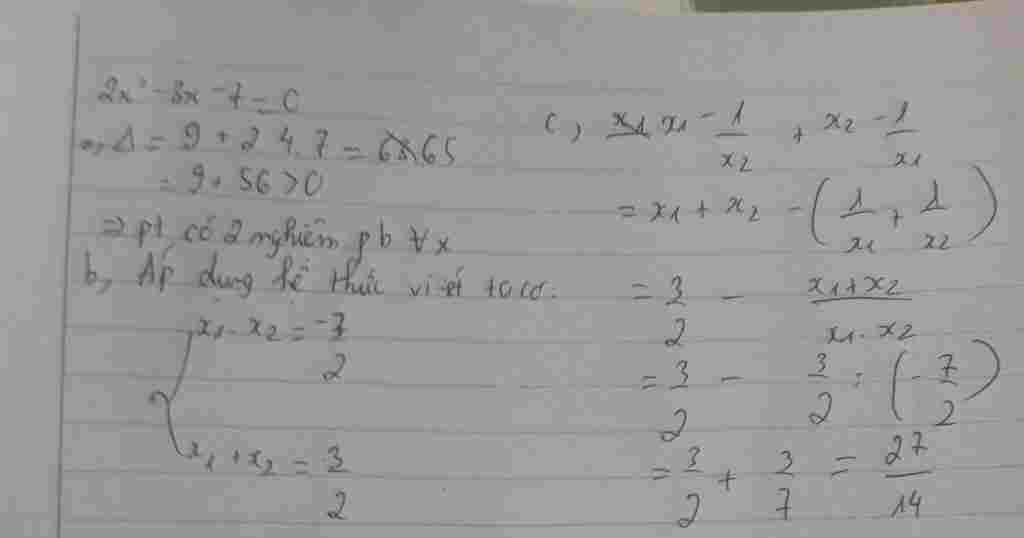
Trả lời 1:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
Giải đáp:
Lời giải và giải thích chi tiết:
a,
2x^2-3x-7=0
Δ=(-3)^2-4.2.(-7)=9+56=65>0
=> Phương trình có hai nghiệm phân biệt x_1; x_2
b,
The hệ thức Viète, ta có: $\begin{cases}x_1+x_2=\dfrac{-b}{a}=\dfrac32\\x_1x_2=\dfrac{c}{a}=\dfrac{-7}{2}\end{cases}$
c,
Theo giả thiết:
\frac{x_1-1}{x_2}+\frac{x_2-1}{x_1}
=\frac{x_1(x_1-1)}{x_1x_2}+\frac{x_2(x_2-1)}{x_1x_2}
=\frac{x_1^2-x_1+x_2^2-x_2}{x_1x_2}
=\frac{(x_1^2+x_2^2)-(x_1+x_2)}{x_1x_2}
=\frac{(x_1+x_2)^2-2x_1x_2-(x_1+x_2)}{x_1x_2}
=\frac{(3/2)^2-2.(-7)/2-3/2}{(-7)/2}
=-31/14





