Câu hỏi:
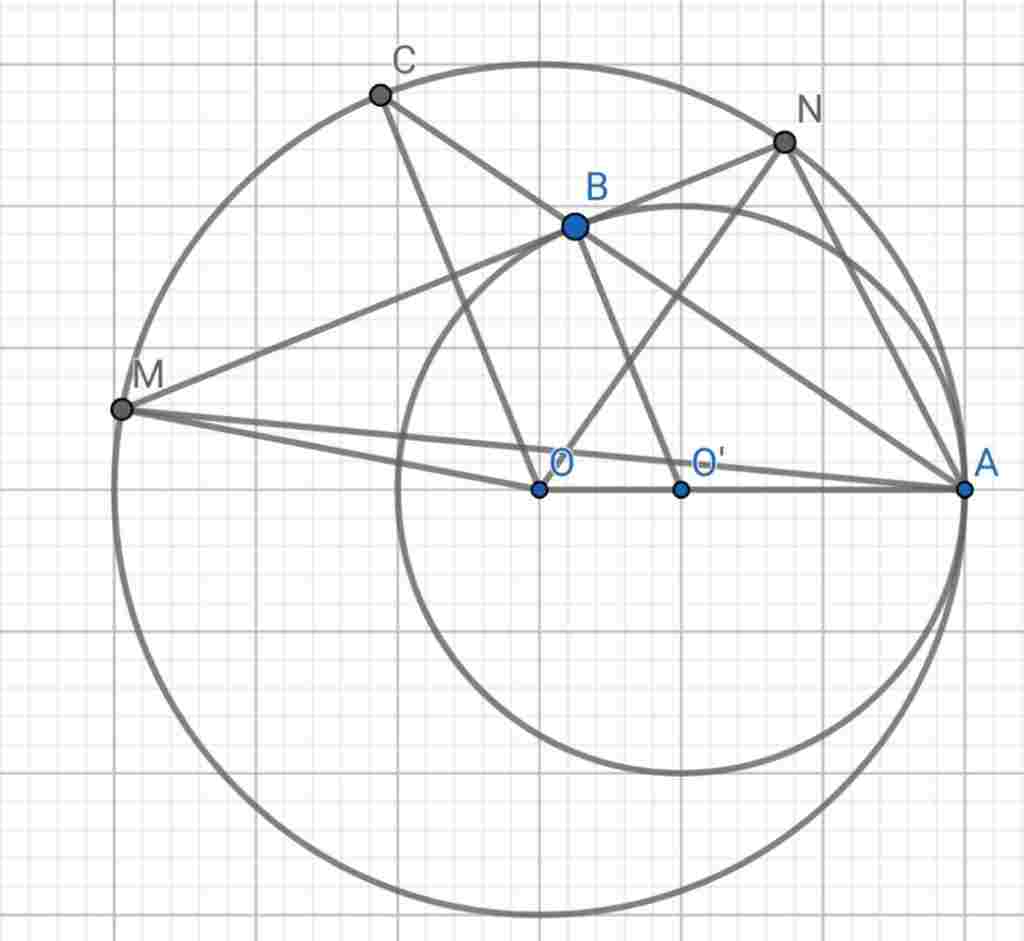
Giúp em bài tập về nhà Toán lớp 9 câu hỏi như sau: Cho hai đường tròn (O; R) và (O’; R’) tiếp xúc trong với nhau tại A, (R > R’). Qua điểm B bất kỳ trên (O’) vẽ tiếp tuyến với (O’) cắt (O) tại hai điểm M và N, AB cắt (O) tại C. Chứng minh rằng:
a) MN ⊥ OC
b) AC là tia phân giác của ∠MAN
Trả lời 2:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
Học tốt nhá !

Trả lời 1:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
a) Ta có: $A;B\in (O’;R’)$
=>O’A=O’B=R’
=>∆O’AB cân tại $O’$
=>\hat{O’BA}=\hat{O’AB} $(1)$
Ta có: $A;C\in (O;R)$
=>OA=OC=R
=>∆OAC cân tại $O$
=>\hat{OCA}=\hat{OAC}=\hat{O’AB} $(2)$
Từ (1);(2)=>\hat{O’BA}=\hat{OCA}
Mà \hat{O’BA} và \hat{OCA}ở vị trí đồng vị
=>O’B//$OC$ $(3)$
Ta lại có $MN$ là tiếp tuyến tại $B$ của $(O’)$
=>O’B$\perp MN$ $(4)$
Từ (3);(4)=>MN$\perp OC$ (đpcm)
$\\$
b) Xét $(O;R)$ có:
\OM=ON=R
=>∆OMN cân tại $O$
Mà MN$\perp OC$ (câu a)
=>MN đồng thời là đường phân giác của \hat{MON}
=>\hat{MOC}=\hat{NOC}
=>\stackrel\frown{CM}=\stackrel\frown{CN} (hai góc ở tâm bằng nhau chắn cung bằng nhau)
Ta lại có:
\hat{MAC}=1/ 2 sđ\stackrel\frown{CM} (góc nội tiếp chắn cung $CM$)
\hat{NAC}=1/ 2 sđ\stackrel\frown{CN} (góc nội tiếp chắn cung $CN$)
=>\hat{MAC}=\hat{NAC}
Mà tia $AC$ nằm giữa hai tia $AM$ và $AN$
=>AC là tia phân giác của \hat{MAN} (đpcm)