Câu hỏi:
Giúp em bài tập về nhà Toán lớp 9 câu hỏi như sau: Cho hàm số y = x-2 có đồ thị (d), hàm số y=3x có đồ thị (d’) và hàm số y=(m-2)x+3 có đồ thị (D).
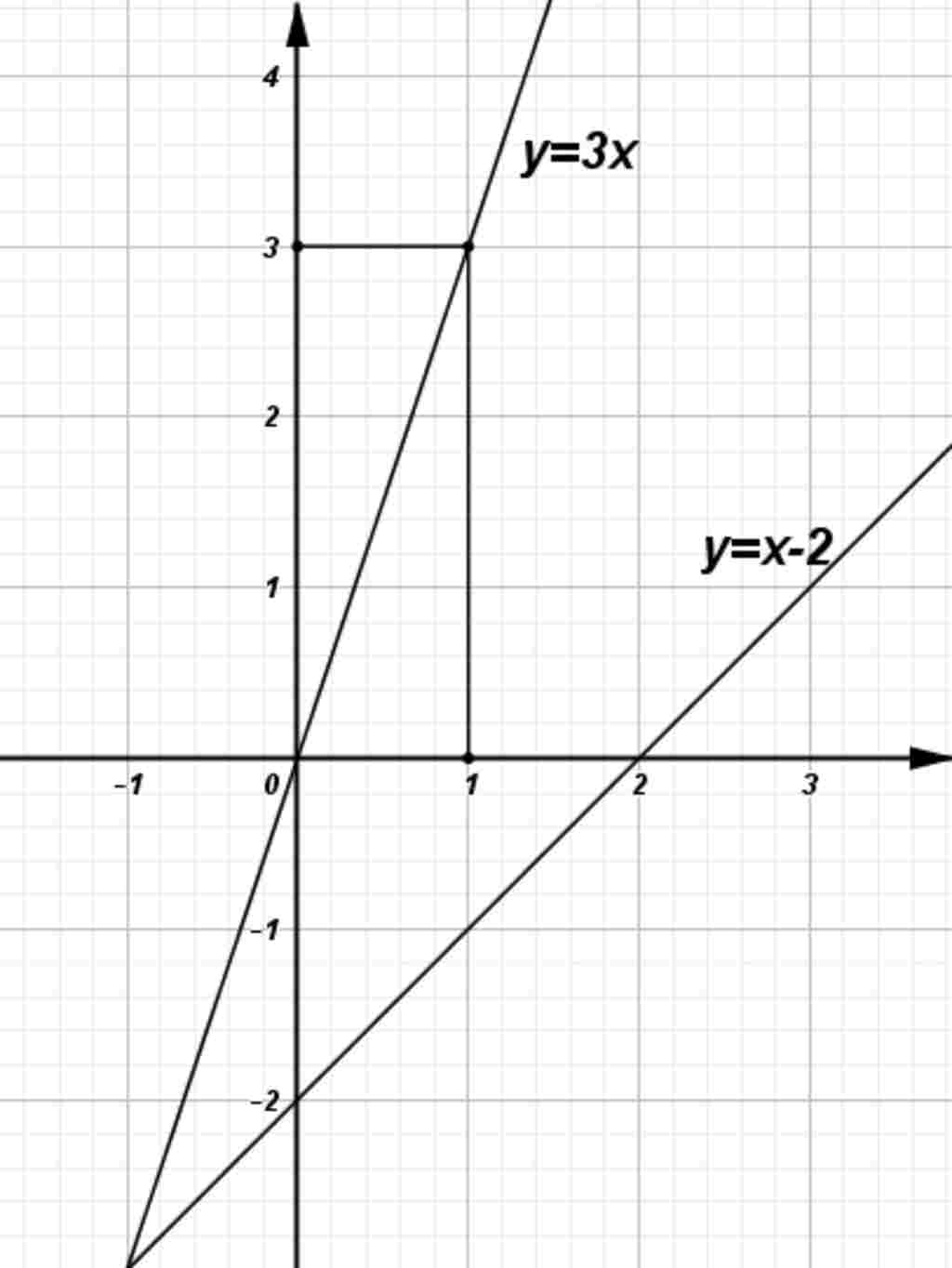
a) Vẽ đồ thị (d) và đồ thị (d’) trên cùng một mặt phẳng tọa độ.
b) Tìm tọa độ giao điểm của đồ thị (d) và đồ thị (d’) bằng phép tính.
c) Tìm m để khoảng cách từ gốc tọa độ O đến đường thằng (D) có giá trị lớn nhất.
Trả lời 1:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
Giải đáp:
a) Lập bảng giá trị ta đượcL
+) (d) đi qua 2 điểm (0;-2) và (2;0)
+) (d’) đi qua 2 điểm (0;0) và (1;3)
b)
Xét pt hoành độ giao điểm của (d) và (d’) ta có:
$\begin{array}{l}
x – 2 = 3x\\
\Rightarrow 3x – x = – 2\\
\Rightarrow 2x = – 2\\
\Rightarrow x = – 1\\
Thay\,vào\,y = 3x \Rightarrow y = – 3
\end{array}$
Vậy giao điểm của chúng là (-1;-3)
c)
Giao điểm của D và 2 trục tọa độ là: A(0;3) và $B\left( {\frac{3}{{2 – m}};0} \right)$
Trong tam giác OAB gọi H là hình chiếu của O lên AB
=> OH chính là khoảng cách từ O đến D
Theo hệ thức lượng trong tam giác vuông ta có:
$\begin{array}{l}
\frac{1}{{O{H^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}} = \frac{1}{{{3^2}}} + \frac{1}{{{{\left( {\frac{3}{{2 – m}}} \right)}^2}}}\\
\Rightarrow \frac{1}{{O{H^2}}} = \frac{1}{9} + \frac{{{{\left( {m – 2} \right)}^2}}}{9} = \frac{{{{\left( {m – 2} \right)}^2} + 1}}{9}\\
\Rightarrow O{H^2} = \frac{9}{{{{\left( {m – 2} \right)}^2} + 1}}\\
Do:{\left( {m – 2} \right)^2} + 1 \ge 1\forall m\\
\Rightarrow \frac{9}{{{{\left( {m – 2} \right)}^2} + 1}} \le 9\forall m\\
\Rightarrow O{H^2} \le 9\\
\Rightarrow OH \le 3\\
\Rightarrow ma{x_{OH}} = 3 \Leftrightarrow m = 2
\end{array}$
Vậy m=2