Câu hỏi:
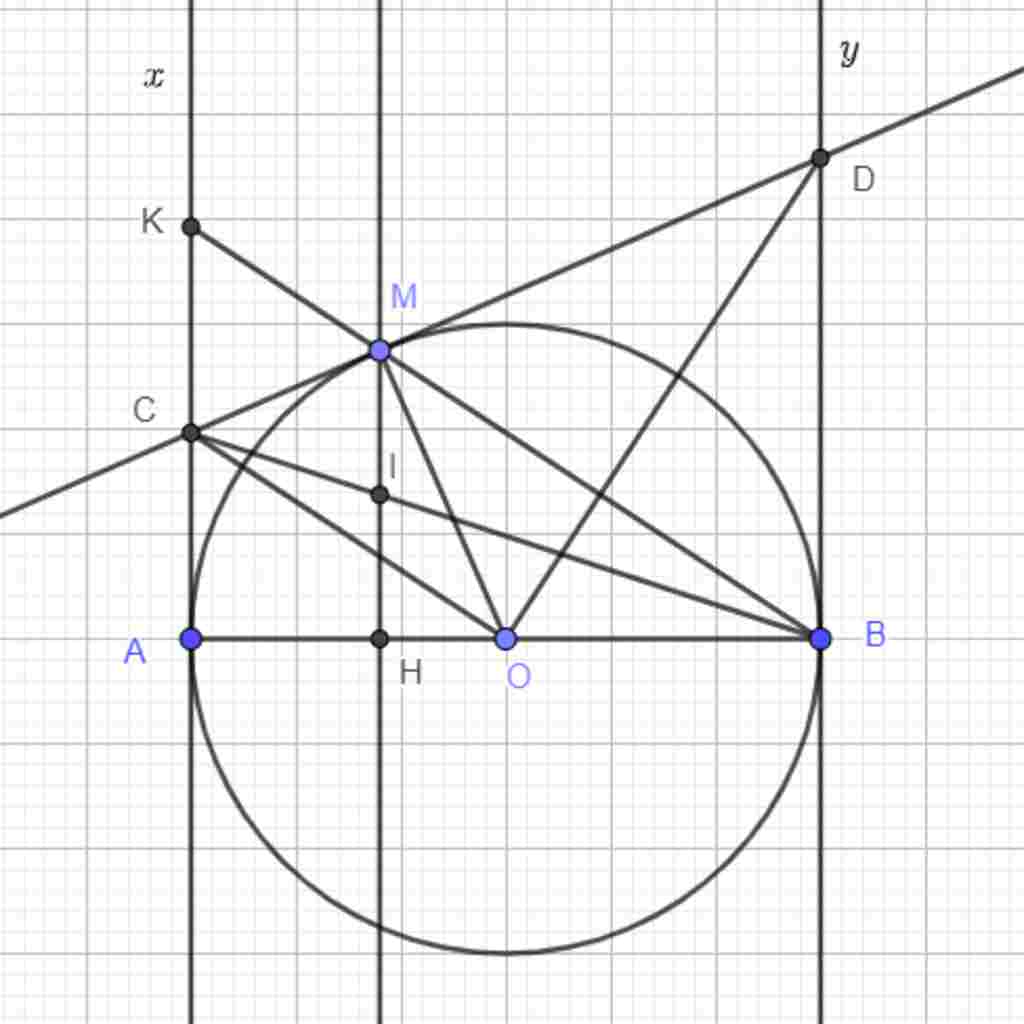
Giúp em bài tập về nhà Toán lớp 9 câu hỏi như sau: Cho nửa đường tròn tâm O có đường kính AB = 2R. Kẻ hai tiếp tuyến Ax, By của nửa đường tròn (O) tại A và B (Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng có bờ là đường thẳng
AB). Qua điểm M thuộc nửa đường tròn (M khác A và B), kẻ tiếp tuyến với nửa đường tròn, cắt tia Ax và By theo thứ tự tại C và D.
a) Chứng minh tam giác COD vuông tại 0;
b) Chứng minh AC.BD=R^2;
c) Kẻ MH vuông góc AB (H ∈ AB). Chứng minh rằng BC đi qua trung điểm của đoạn MH.
Trả lời 1:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
Lời giải và giải thích chi tiết:
a.Vì CM, CA là tiếp tuyến của O
$\rightarrow $ OC là phân giác $\widehat{MOA}$
Tương tự ta chứng minh được OD là phân giác $\widehat{MOB}$
Do $\widehat{MOA}+\widehat{MOB}=\widehat{AOB}=180^o$
$\rightarrow \dfrac{1}{2}.\widehat{MOA}+\dfrac{1}{2}.\widehat{MOB}=90^o$
$\rightarrow \widehat{MOC}+\widehat{MOD}=90^o$
$\rightarrow \widehat{COD}=90^o$
$\rightarrow \Delta COD$ vuông tại O
b.Vì CD là tiếp tuyến của (O)
$\rightarrow OM\perp CD $ Mà $ \Delta OCD, OC\perp OD$
$\rightarrow CM.DM=OM^2$
Mà $CM=CA, DM=DA$ (do $CA, CM$ là tiếp tuyến của $(O); DM, DA$ là tiếp tuyến của $(O)$
$\rightarrow AC.BD=R^2(OM=R)$
$\rightarrow đpcm$
c.Gọi $MH\cap BC=I, MB\cap AC=K$
Vì DM,DB là tiếp tuyến của (O)
$\rightarrow MB\perp OD$
$\rightarrow OC// MB(OC\perp OD)\rightarrow OC// BK$
$\rightarrow OC$ là đường trung bình $\Delta ABK, O$ là trung điểm AB
$\rightarrow C$ là trung điểm AK$\rightarrow CK = CA$
$\rightarrow \dfrac{MI}{CK}=\dfrac{BI}{BC}=\dfrac{IH}{AC}$
$\rightarrow MI=IH(CK=CA)$
$\rightarrow I$ là trung điểm $MH$
$\rightarrow BC$ đi qua trung điểm của đoạn $MH$
$\rightarrow đpcm$