Câu hỏi:
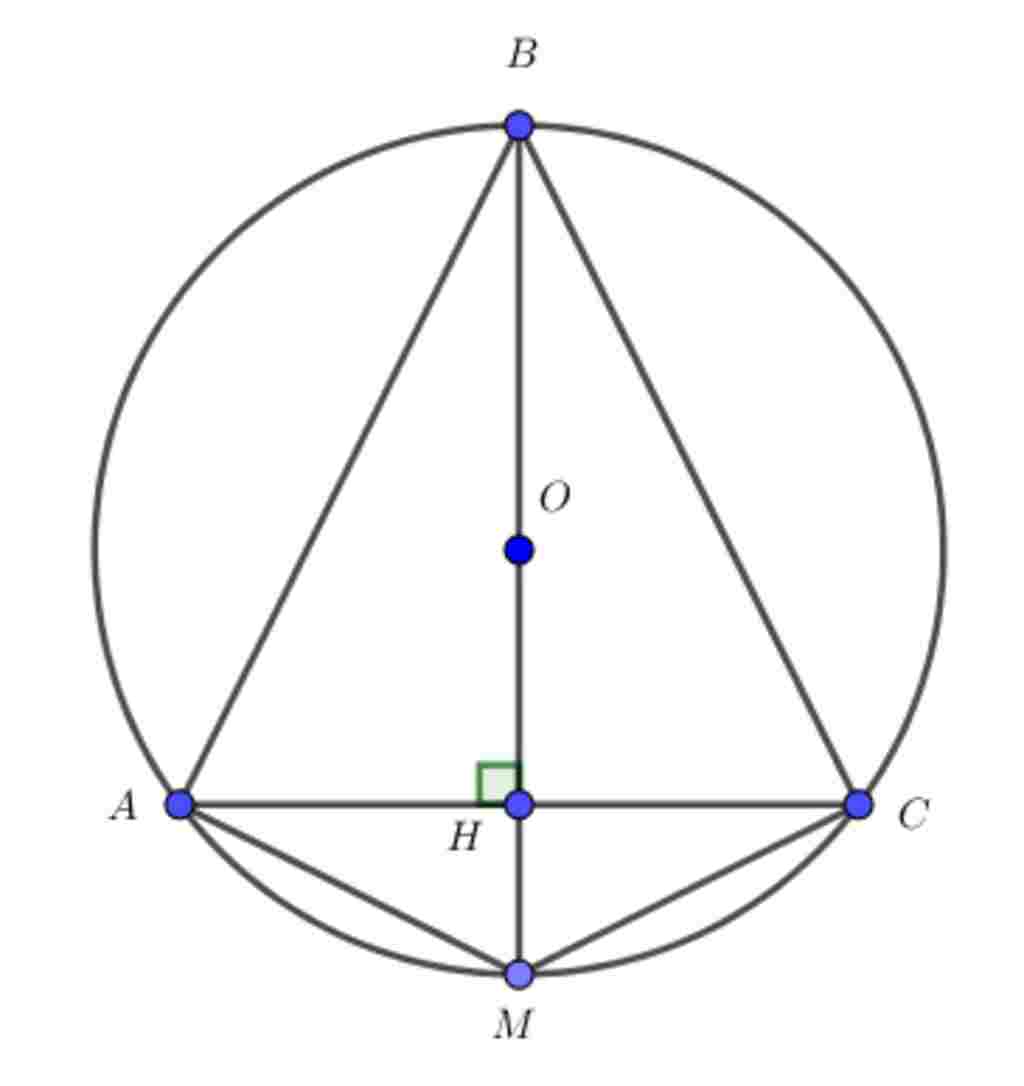
Giúp em bài tập về nhà Toán lớp 9 câu hỏi như sau: Cho tam giác ABC cân tại B, nội tiếp đường tròn (O). Đường cao BH cắt đường tròn (O) tại M (M≠B)
a, chứng minh tam giác BCM vuông tại C
b, cho AC = 24cm, BC = 20cm. Tính đường cao BH và bán kính đường tròn (O).
c, Chứng minh góc ACB = góc AMB
Trả lời 1:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
Giải đáp:
a)
Xét tam giác $ABC$ cân tại $B$ có đường cao $BH$
$\Rightarrow BH$ đồng thời là đường trung trực
hay $BM$ là trung trực của $AC$
$\Rightarrow O \in BM$
$\Rightarrow BM$ là đường kính của đường tròn $(O)$.
Xét tam giác $BCM$ nội tiếp đường tròn tâm $(O)$, có $BM$ là đường kính
$OC=OB=OM=\dfrac{1}{2}BM$ (trong tam giác đường trung tuyến ứng với một cạnh bằng nửa cạnh đó thì tam giác đó là tam giác vuông tại đỉnh của đường trung tuyến)
$\Rightarrow$ tam giác $BCM$ vuông tại $C$
b)
Do $BH$ là đường trung trực nên $H$ là trung điểm của $AC$
$\Rightarrow AH=HC=\dfrac{1}{2}\cdot AC=\dfrac{1}{2}\cdot 24=12cm$
Xét tam giác $BCH$ vuông tại $H$ có
$BH^2+HC^2=BC^2$ (định lý Pitago)
$BH^2=BC^2-HC^2=20^2-12^2=256$
$BH=16cm$
Xét tam giác $BCM$ vuông tại $C$ có đường cao $HC$, nên theo hệ thức lượng trong tam giác vuông ta có:
$BC^2=BH.BM$
$BM=\dfrac{BC^2}{BH}=\dfrac{20^2}{16}=25cm$
Vậy bán kính của đường tròn tâm $(O)$ là: $R=\dfrac{1}{2}BM=\dfrac{1}{2}\cdot 25=12,5cm$.
c)
Chứng minh tương tự câu a ta được $\Delta BAM\bot A$
$\Rightarrow\widehat{AMB}+\widehat{ABM}=90^o$
mà $CH\bot BH\Rightarrow\widehat{ACB}+\widehat{CBM}=90^o$
mà $\widehat{ABM}=\widehat{CBM}$ do $\Delta ABC$ cân đỉnh $B$ nên đường cao $BH$ cũng là đường phân giác
$\Rightarrow\widehat{AMB}=\widehat{ACB}$