Câu hỏi:
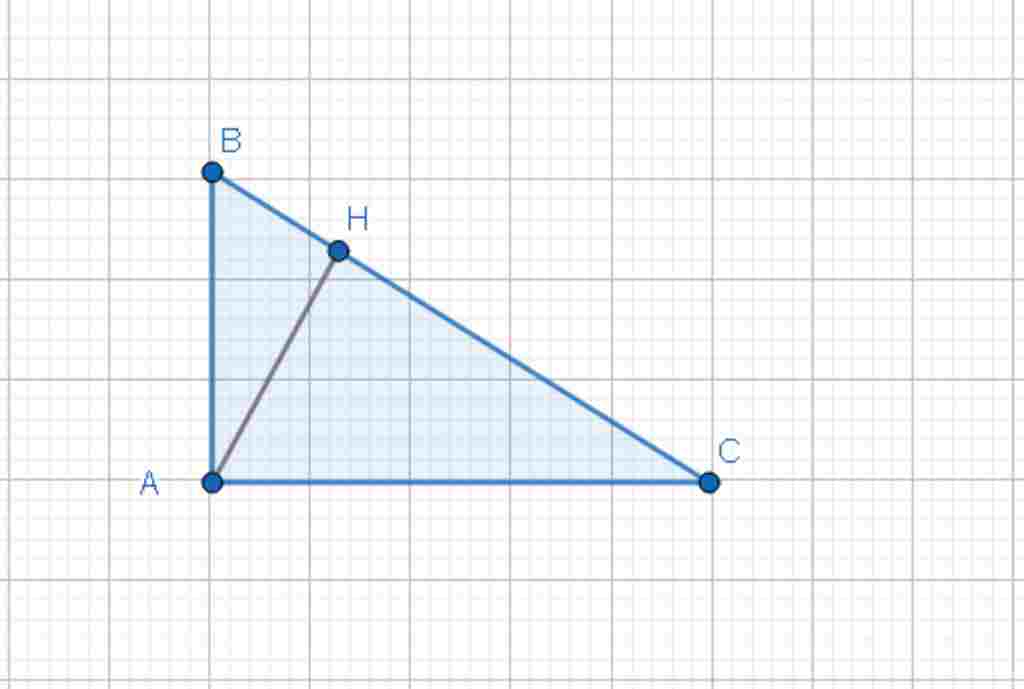
Giúp em bài tập về nhà Toán lớp 9 câu hỏi như sau: tam giác ABC vuông tại A có BC = 5 cm AC bằng 4 cm đường cao AH Tính sin B và và độ dài các đoạn thẳng CH, AH
Trả lời 2:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
Giải đáp:áp dụng đl pitago vào tgv ABC có :
BC2 = AB2+AC2
thay AC = 4 cm , BC = 5cm vào ta được:
25 = AC2+16
=> AB = căn bậc hai của 9
=> AB = 3cm
áp dụng hệ thức về cạnh và đường cao trong tgv ABC ta có :
1/AH2=1/AB2+1/AC2
<=> 1/AH2 = 1/3 MŨ 2 + 1/4 MŨ 2
<=> 1/AH2 = 1/9 + 1/16
<=> 1/AH2 = 25/144
<=> AH2 = CĂN BẬC HAI CỦA 144/25
<=> AH = 2,4 cm
áp dụng đl pitago vào tgv AHC có :
AC2 = AH2 + HC2
<=> 4 BÌNH PHƯƠNG = ( 2,4 ) BÌNH PHƯƠNG + HC2
<=> HC2 = 16-144/25
<=> HC2 = 256/25
<=> HC = CĂN BẬC HAI CỦA 256/25
=> HC = 3,2 CM
VẬY AH = 2,4 CM ; HC = 3,2 CM
Lời giải và giải thích chi tiết:
Trả lời 1:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
Giải đáp:
sinB≈sin53°
CH=3,2 cm;AH=2,4cm
Lời giải và giải thích chi tiết:
Xét ΔvABC có:
sinB=(AC)/(BC)=4/5=0,8
⇒sinB≈sin53°
Xét ΔvABC có AH là đường cao
⇒AC^2=CH.BC (hệ thức lượng)
⇒4^2=CH.5
⇒CH=(4^2)/5=16/5=3,2(cm)
Có AH^2=AC^2-CH^2 (pytago)
⇒AH^2=4^2-(3,2)^2=5,76
⇒AH=2,4(cm)