Câu hỏi:
Giúp em bài tập về nhà Toán lớp 9 câu hỏi như sau: Cho các hàm số y = x – 1 (d1) ; y = -x – 3 (d2) và y = mx + m – 1 (d3)
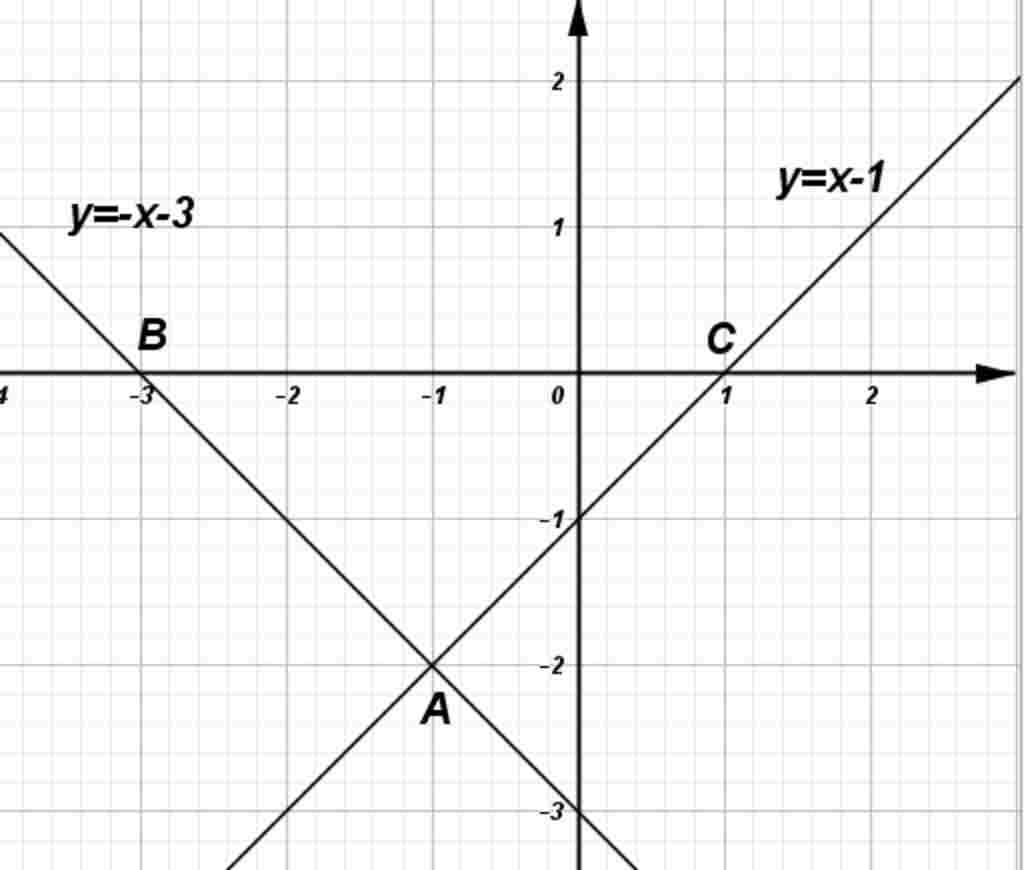
a) Vẽ (d1) và (d2) trên cùng một mặt phẳng toạ độ
b) Tìm toạ độ giao điểm của 2 đường thẳng (d1) và (d2)
c) Tìm m để (d1) cắt (d3) tại một điểm trên trục tung
d) Tìm giá trị của m để 3 đường thẳng trên đồng quy
e) Tính chu vi và diện tích của tam giác giới hạn bởi (d1) , (d2) và trục hoành
f) Tìm khoảng cách từ gốc toạ độ đến (d1)
Trả lời 1:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
Giải đáp:
a) + y=x-1
– Cho x=0 => y=-1
– Cho x=1 => y=0
=> (d1) là đường thẳng đi qua 2 điểm (0;-1) và (1;0)
+ y=-x-3
– Cho x=0 => y=-3
– Cho x=-3 => y=0
=> (d2) là đường thẳng đi qua 2 điểm (0;-3) và (-3;0)
b) Xét pt hoành độ giao điểm của d1 và d2
$\begin{array}{l}
x – 1 = – x – 3\\
\Rightarrow x + x = – 3 + 1\\
\Rightarrow 2x = – 2\\
\Rightarrow x = – 1\\
\Rightarrow y = x – 1 = – 1 – 1 = – 2\\
\Rightarrow \left( {{d_1}} \right) \cap \left( {{d_2}} \right) = \left( { – 1; – 2} \right)
\end{array}$
c) d1: cho x=0 => y=-1
Do d1 cắt d3 tại 1 điểm trên trục tung nên d3 đi qua điểm (0;-1)
$\begin{array}{l}
\Rightarrow – 1 = m – 1\\
\Rightarrow m = 0
\end{array}$
Vậy m=0
d) 3 đường thẳng đồng quy thì d3 đi qua giao điểm của d1 và d2
$\begin{array}{l}
\Rightarrow \left( { – 1; – 2} \right) \in \left( {{d_3}} \right)\\
\Rightarrow – 2 = m.\left( { – 1} \right) + m – 1\\
\Rightarrow – 2 = – 1\left( {ktm} \right)
\end{array}$
Vậy ko có m để 3 đường thẳng đồng quy
e)
Gọi A (-1;-2), B,C lần lượt là giao của d2, d1 với Ox
=> tam giác giới hạn bởi d1, d2 với trục hoành là ABC
$\begin{array}{l}
BC = 4;{h_a} = 2\\
\Rightarrow {S_{ABC}} = \dfrac{1}{2}.4.2 = 4
\end{array}$
$\begin{array}{l}
AB = AC = \sqrt {{2^2} + {2^2}} = 2\sqrt 2 \\
\Rightarrow Chu\,vi = 2.2\sqrt 2 + 4 = 4\sqrt 2 + 4
\end{array}$
f) Khoảng cách từ O đến d1 là đường cao của tam giác vuông cân cạnh bằng 1
$ \Rightarrow d = \dfrac{{1.1}}{{\sqrt 2 }} = \dfrac{1}{{\sqrt 2 }} = \dfrac{{\sqrt 2 }}{2}$