Câu hỏi:
Giúp em bài tập về nhà Toán lớp 9 câu hỏi như sau: Cho tam giác ABC, BC = a, AC = b, AB= c, p = a+b+c/2
r,ra,rb,rc là bán kính đường tròn nội tiếp, bàng tiếp trong góc A,B,C của tam giác ABC
CMR SABC= (p-a)*ra
Trả lời 1:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
Giải đáp:
Lời giải và giải thích chi tiết: Giải theo $L9$
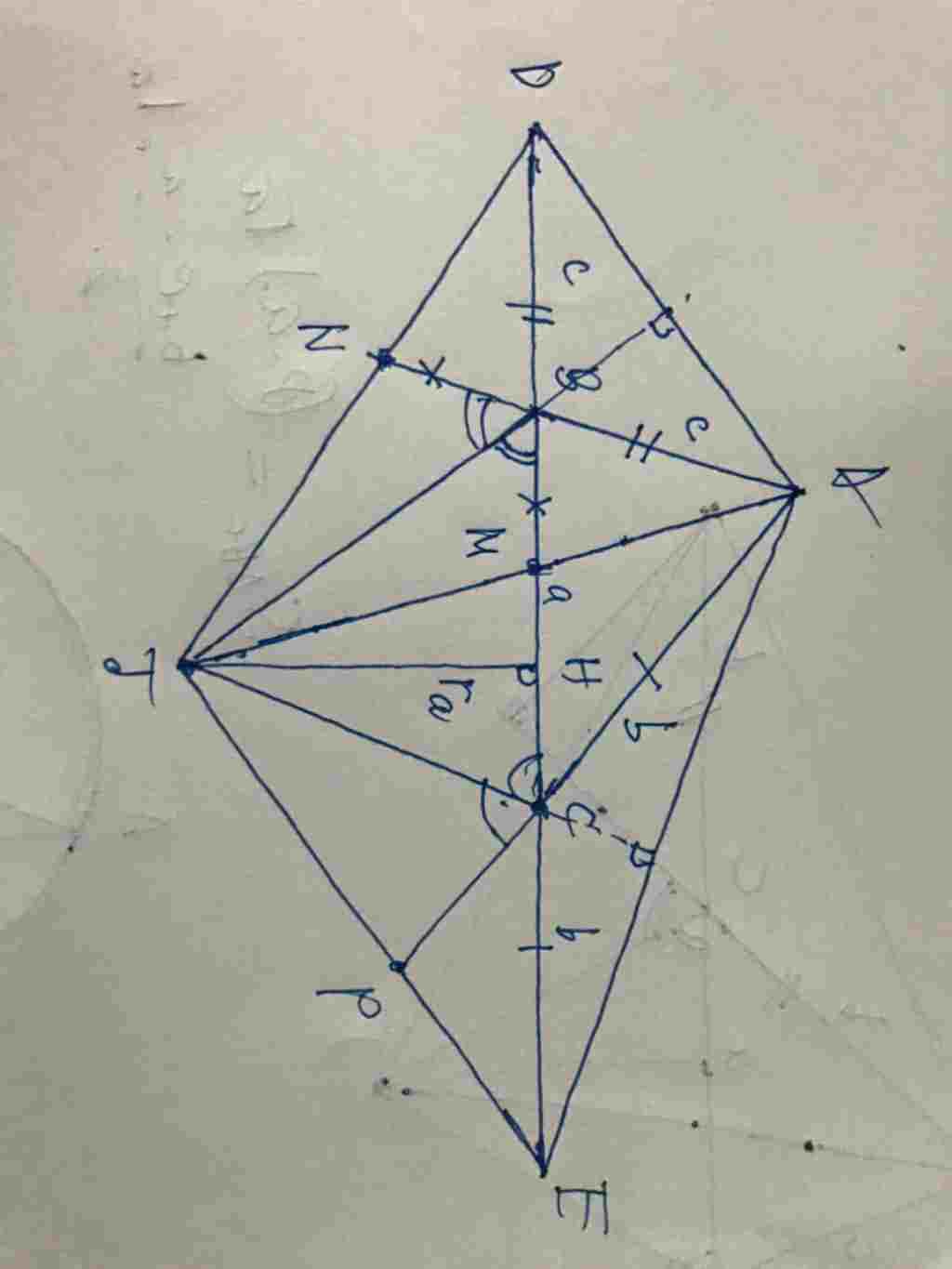
Trên tia đối của tia $BC$ lấy $D$ sao cho $DB = AB = c (1)$
Trên tia đối của tia $CB$ lấy $E$ sao cho $EC = AC = b(2)$
Gọi $J $ là tâm đường tròn bàng tiếp trong góc $A$
$AJ$ cắt $BC$ tại $M; DJ$ cắt $AB$ tại $M$;
$EJ$ cắt $AC$ tại $P$. Vẽ $JH⊥BC$ tại $H ⇒ JH = r_{a}$
Từ $(1) ⇒ ΔABD$ cân tại $B$ mà $BJ$ là phân giác
$∠MBN ⇒ BJ$ là trung trực của $AD$
$ ⇒ ΔABM = ΔDBN ⇒ S_{ΔABM} = S_{ΔDBN}(3)$
$ ΔJBM = ΔJBN ⇒ S_{ΔJBM} = S_{ΔJBN}(4)$
Tương tự:
$ ⇒ ΔACM = ΔECP ⇒ S_{ΔACM} = S_{ΔECP}(5)$
$ ΔJCM = ΔJCP ⇒ S_{ΔJCM} = S_{ΔJCP}(6)$
$(3) + (5) + (4) + (6)$ vế với vế :
$ (S_{ΔABM} + S_{ΔACM}) + (S_{ΔJBM} + S_{ΔJCM})$
$ = (S_{ΔDBN} + S_{ΔJBN}) + (S_{ΔECP} + S_{ΔJCP}) $
$ ⇔ S_{ΔABC} + S_{ΔJBC} = S_{ΔJBD} + S_{ΔJCE}$
$ ⇔ S_{ΔABC} = S_{ΔJBD} + S_{ΔJCE} – S_{ΔJBC} $
$ ⇔ S_{ΔABC} = \dfrac{BD + CE – BC}{2}.JH $
$ ⇔ S_{ΔABC} = \dfrac{b + c – a}{2}r_{a} $
$ ⇔ S_{ΔABC} = \dfrac{(a + b + c) – 2a}{2}r_{a} $
$ ⇔ S_{ΔABC} = (p – a)r_{a} (đpcm)$