Câu hỏi:
Giúp em bài tập về nhà Toán lớp 9 câu hỏi như sau: Cho tam giác ABC vuông tại A có đường cao Ah chia cạnh huyền BC thành hai đoạn BH=4cm và HC=6cm
a, Tính độ dài các đoạn AH , AB , AC
b, Gọi M là trung điểm của AC
Tính số đo góc AMB ( làm tròn đến độ )
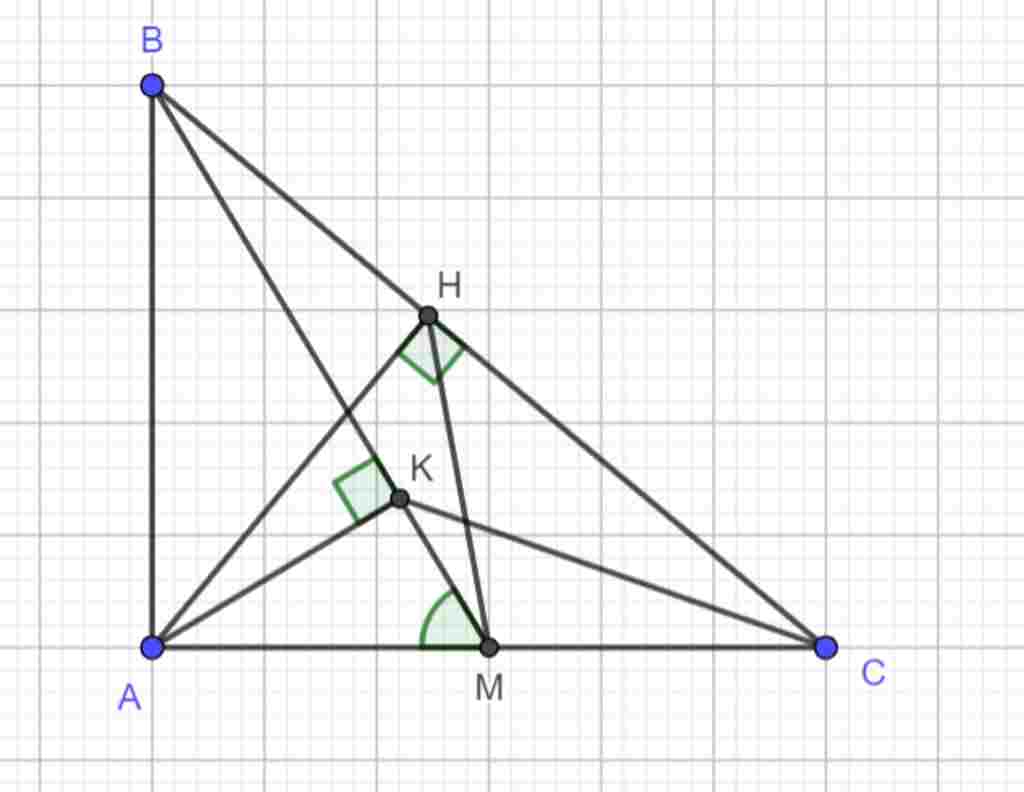
c, Kẻ AK vuông góc với BM
Giúp mk vs mn
Trả lời 2:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
a) $AH^2=BH.HC⇒AH=\sqrt{4.6}=\sqrt{24}⇒AH=2\sqrt{6}$ (cm)
$AB=\sqrt{AH^2+BH^2}=\sqrt{(2\sqrt{6})^2+4^2}=2\sqrt{10}$ (cm)
$AC=\sqrt{AH^2+HC^2}=\sqrt{(2\sqrt{6})^2+6^2}=2\sqrt{15}$ (cm)
b) $AM=\dfrac{1}{2}AC=\dfrac{2\sqrt{15}}{2}=\sqrt{15}$
Áp dụng hệ thức lượng giác vào $\Delta ABM$ có:
$\tan \widehat{AMB}=\dfrac{AB}{AM}=\dfrac{2\sqrt{10}}{\sqrt{15}} \Rightarrow \widehat{AMB}=58,518^o≈59^o$
c) Áp dụng định lý Pitago ta có: $BM=\sqrt{AB^2+AM^2}=\sqrt{55}$
$AB^2=BK.BM⇒BK=\dfrac{AB^2}{BM}=\dfrac{40}{\sqrt{55}}$
Ta có: $\widehat {KBC}=\widehat{HBM}$ đều là một góc
$\dfrac{BK}{BH}=\dfrac{40}{\sqrt{55}.4}=\dfrac{10}{\sqrt{55}}$
Mà $\dfrac{BC}{BM}=\dfrac{10}{\sqrt{55}}⇒\dfrac{BK}{BH}=\dfrac{BC}{BM}=\dfrac{10}{\sqrt{55}}$
$\Rightarrow ΔBKC\sim Δ BHM$ (c.g.c)
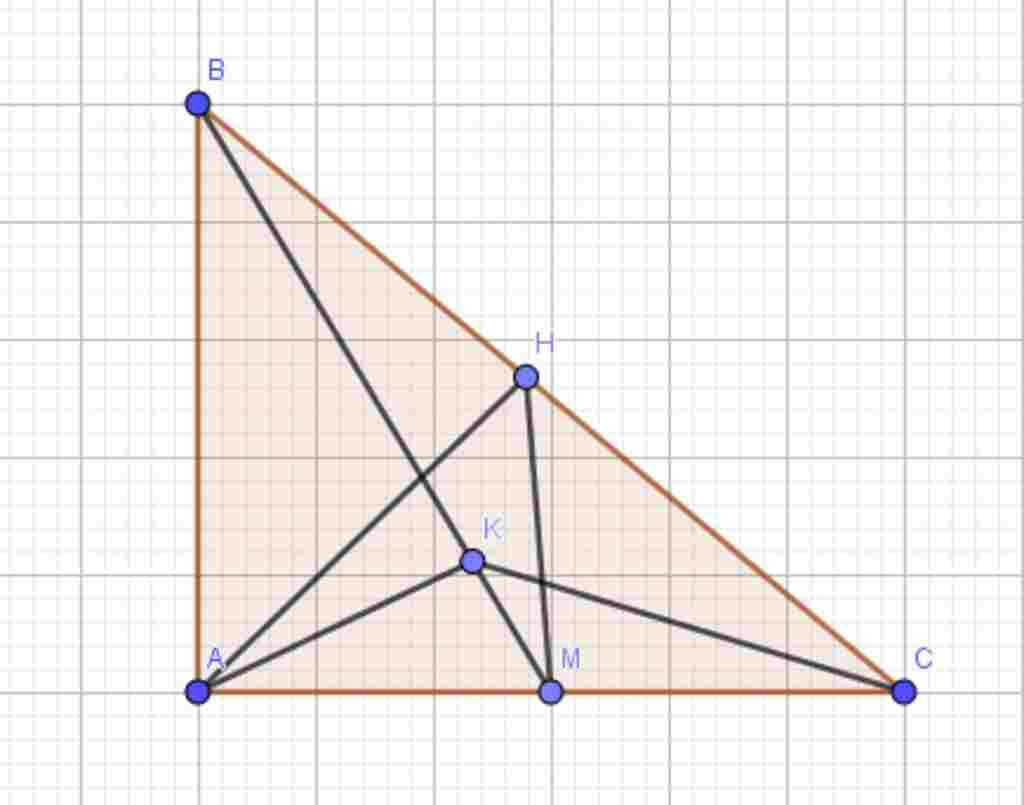
Trả lời 1:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
a) $BC=BH+HC=4+6=10$cm
Áp dụng hệ thức lượng vào $\Delta ABC\bot A$ đường cao $AH$
$AH^2=BH.HC=4.6=24\Rightarrow AH=2\sqrt6$cm
$AB^2=BH.BC=4.10=40\Rightarrow AB=2\sqrt{10}$cm
$AC^2=HC.BC=6.10=60\Rightarrow AC=2\sqrt{15}$cm
b) $AM=\dfrac{AC}2=\sqrt{15}$
$\Delta AMB\bot A$ có $\tan\widehat{AMB}=\dfrac{AB}{AM}=\dfrac{2\sqrt{10}}{\sqrt{15}}$
$\Rightarrow\widehat{AMB}\approx59^o$
c) Áp dụng định lý Pitago vào $\Delta ABM\bot A$ có:
$BM^2=AB^2+AM^2=55\Rightarrow BM=\sqrt{55}$
Áp dụng hệ thức lượng vào $\Delta ABM\bot A$ có:
$AB^2=BK.BM\Rightarrow BK=\dfrac{AB^2}{BM}=\dfrac{40}{\sqrt{55}}$
$\Delta BKC$ và $\Delta BHM$ có:
$\widehat {KBC}=\widehat{HBM}$ cùng là một góc
$\dfrac{BK}{BH}=\dfrac{\dfrac{40}{\sqrt{55}}}{4}=\dfrac{10}{\sqrt{55}}=\dfrac{BC}{BM}$
$\Rightarrow\Delta BKC\sim\Delta BHM$ (c.g.c)