Câu hỏi:
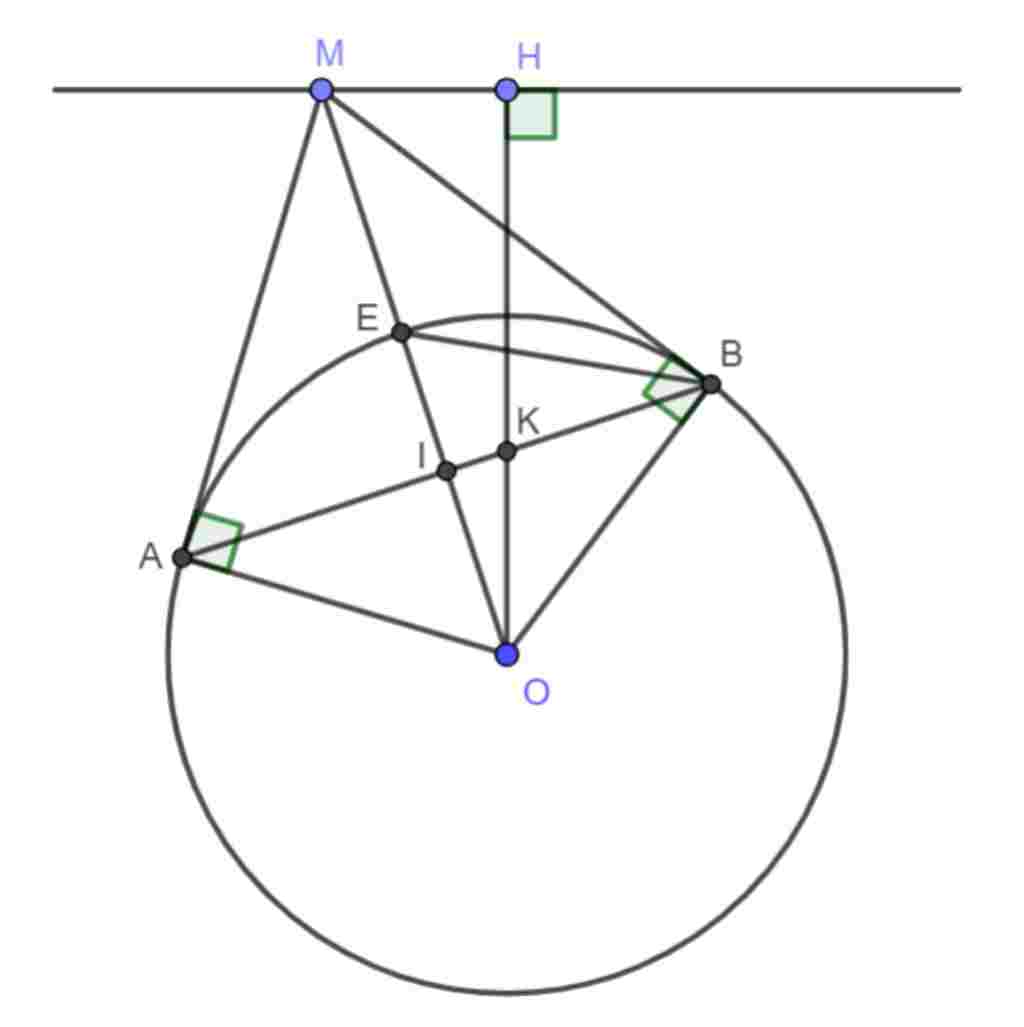
Giúp em bài tập về nhà Toán lớp 9 câu hỏi như sau: Cho đường tròn (O,R) và đường thẳng d cố định, d không có điểm chung với đường tròn. Gọi M là điểm thuộc đường thẳng d. Qua M kẻ hai tiếp tuyến MA,MB với đường tròn (A,B là các tiếp điểm). Từ O kẻ OH vuông góc với đường thẳng d (H thuộc d). Nối A với B, AB cắt OH tại K và cắt OM taị I. Tia OM cắt (O;R) tại E
a) Chứng minh rằng năm điểm A, O, B, H, M cùng thuộc một đường tròn.
b) Chứng minh rằng OK. OH=OI.OM
c) Chứng minh E là tâm đường tròn nội tiếp tam giác MAB
Trả lời 1:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
a) Xét tứ giác $OAMB$ có:
$\widehat{OAM} + \widehat{OBM} = 180^o$
Do đó $OAMB$ là tứ giác nội tiếp
Ta lại có: $\widehat{OAM} = \widehat{OBM} = 90^o$
$\Rightarrow OM$ là đường kính của đường tròn ngoại tiếp tức giác $OABM$
$\Rightarrow O,A,M,B$ cùng thuộc đường tròn đường kính $OM$ $(1)$
Xét tứ giác $OAHM$ có:
$\widehat{OAM} = \widehat{OHM} = 90^o$
Do đó $OAHM$ là tứ giác nội tiếp đường tròn đường kính $OM$
$\Rightarrow O,A,H,M$ cùng thuộc đường tròn đường kính $OM$ $(2)$
$(1)(2)\Rightarrow A,O,B,H,M$ cùng thuộc một đường tròn
b) Ta có: $MA, MB$ là tiếp tuyến của $(O)$ tại $A$ và $B$
$\Rightarrow MA = MB$
mà $OA = OB = R$
nên $OM$ là trung trực của $AB$
$\Rightarrow OM\perp AB$
$\Rightarrow \widehat{I} = 90^o$
Xét $ΔOIK$ và $ΔOHM$ có:
$\widehat{O}:$ góc chung
$\widehat{OIK} = \widehat{OHM} = 90^o$
Do đó $ΔOIK\sim ΔOHM \, (g.g)$
$\Rightarrow \dfrac{OI}{OH} = \dfrac{OK}{OM}$
$\Rightarrow OK.OH = OI.OM$
c) Xét $ΔMAB$ cân tại $M$ $(MA= MB)$
có $MO$ là trung trực của $AB$
$\Rightarrow MO$ là phân giác của $\widehat{AMB}$ $(3)$
Ta cũng có: $OM$ là trung trực của $\widehat{AOB}$ trong $ΔOAB$ cân tại $O$
$\Rightarrow \widehat{AOE} = \widehat{BOE}$ nên cung AE = cung BE
$\Rightarrow \widehat{ABE} = \widehat{MBE}$ (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn hai cung bằng nhau) (cung AE=cung BE)
$\Rightarrow BE$ là phân giác của $\widehat{ABM}$ $(4)$
$(3)(4)\Rightarrow E$ là tâm đường tròn nội tiếp $ΔMAB$