Câu hỏi:
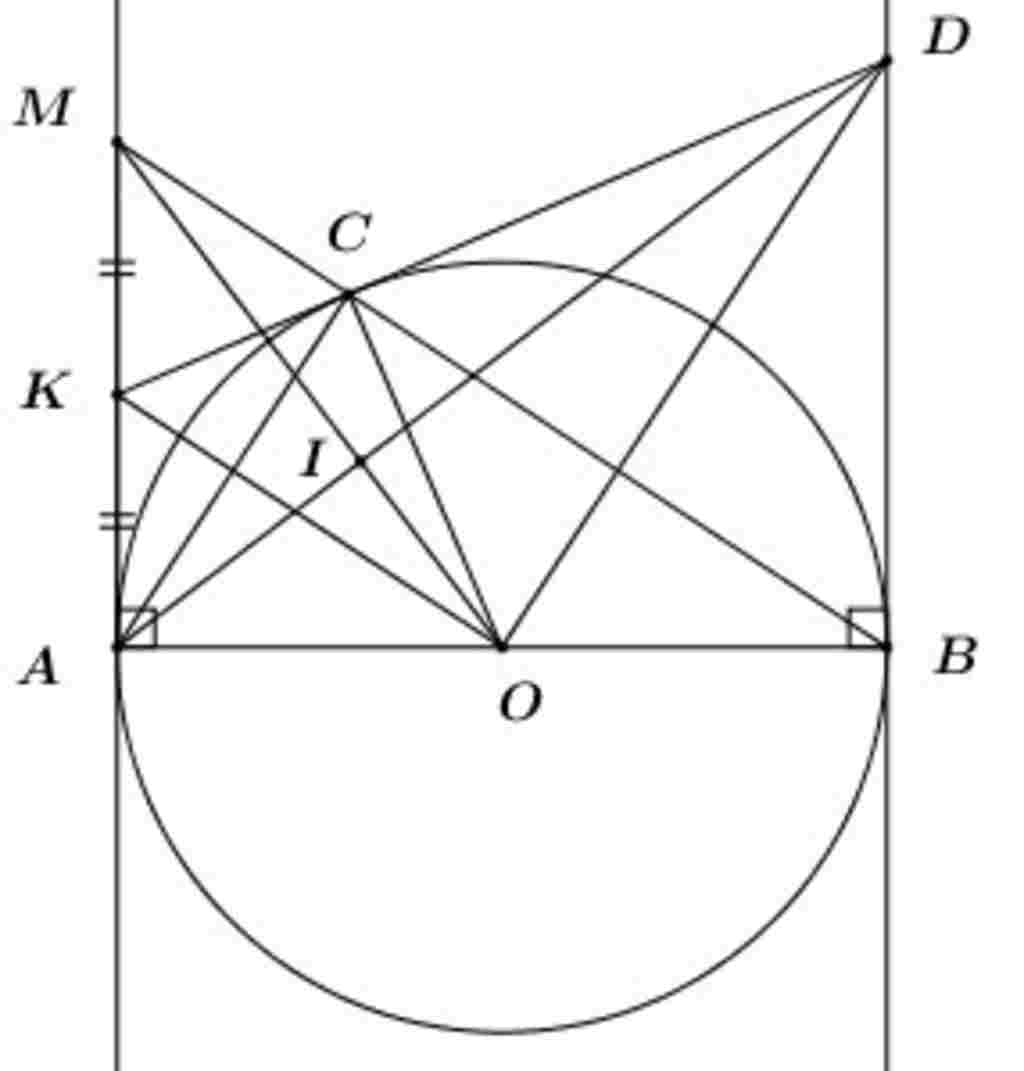
Giúp em bài tập về nhà Toán lớp 9 câu hỏi như sau: Cho đường tròn (O;R), đường kính AB. Lấy C thuộc đường tròn (O) (C khác A và B). Tiếp tuyến tại A của đường tròn (O) cắt đường thẳng BC tại M.
a) Chứng minh: tam giác ABC là tam giác vuông và 4R^2= BC.BM
b) Gọi K là trung điểm MA. Chứng minh: KC là tiếp tuyến của (O)
c) Tia KC cắt tiếptiếp tuyến tại B của đường tròn (O) tại D, chứng minh: MO vuông góc AD
Trả lời 1:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
Giải đáp:
Bạn tham khảo nhé!
Lời giải và giải thích chi tiết:
a) Xét tam giác ABC có: \(OC = \frac{1}{2}AB\,\,\left( { = R} \right)\)
\( \Rightarrow \Delta ABC\) vuông tại C (Tam giác có trung tuyến ứng với 1 cạnh bằng nửa cạnh ấy).
Xét tam giác vuông ABM, đường cao AC có:
\(A{B^2} = BC.BM\) (hệ thức lượng)
\( \Rightarrow {\left( {2R} \right)^2} = BC.BM \Rightarrow 4{R^2} = BC.BM\).
b) Xét tam giác vuông ACM có: \(KC = \frac{1}{2}AM = KA = KM\) (trung tuyến ứng với cạnh huyền trong tam giác vuông).
\( \Rightarrow \Delta KAC\) cân tại \(A \Rightarrow \widehat {KAC} = \widehat {KCA}\) (2 góc ở đáy).
Tam giác OAC có \(OA = OC \Rightarrow \Delta OAC\) cân tại \(O \Rightarrow \widehat {OAC} = \widehat {OCA}\) (2 góc ở đáy).
\( \Rightarrow \widehat {OCK} = \widehat {OCA} + \widehat {KCA} = \widehat {OAC} + \widehat {KAC} = \widehat {OAK} = {90^0}\).
\( \Rightarrow KC \bot OC \Rightarrow KC\) là tiếp tuyến của (O) tại C.
c) Áp dụng tính chất 2 tiếp tuyến cắt nhau ta có: OK, OD lần lượt là phân giác góc \(\widehat {AOC},\,\,\widehat {BOC}\).
\( \Rightarrow OK \bot OD\) (phân giác của 2 góc kề bù) \( \Rightarrow \Delta KOD\) vuông tại O.
Lại có \(BD = CD\).
\( \Rightarrow AM.BD = 2CK.CD = 2.O{C^2} = 2{R^2}\) (Hệ thức lượng).
Ta có: \(OA.AB = R.2R = 2{R^2}\).
\( \Rightarrow OA.AB = AM.BD\).
\( \Rightarrow \frac{{OA}}{{BD}} = \frac{{AM}}{{AB}}\).
Xét tam giác OAM và tam giác DBA có:
\(\widehat {OAM} = \widehat {DBA} = {90^0}\);
\(\frac{{OA}}{{BD}} = \frac{{AM}}{{AB}}\,\,\left( {cmt} \right)\)
\( \Rightarrow \Delta OAM \sim \Delta DBA\,\,\left( {c.g.c} \right) \Rightarrow \widehat {AOM} = \widehat {BDO}\)
Gọi I là giao điểm của MO và AD.
Xét tam giác OAI có:
\(\widehat {IAO} + \widehat {IOA} = \widehat {IAO} + \widehat {AOM} = \widehat {IAO} + \widehat {BDO} = {90^0}\) (do tam giác ABD vuông tại B)
\( \Rightarrow \Delta OAI\) vuông tại I \( \Rightarrow AI \bot OI\) hay \(MO \bot AD\) (đpcm).