Câu hỏi:
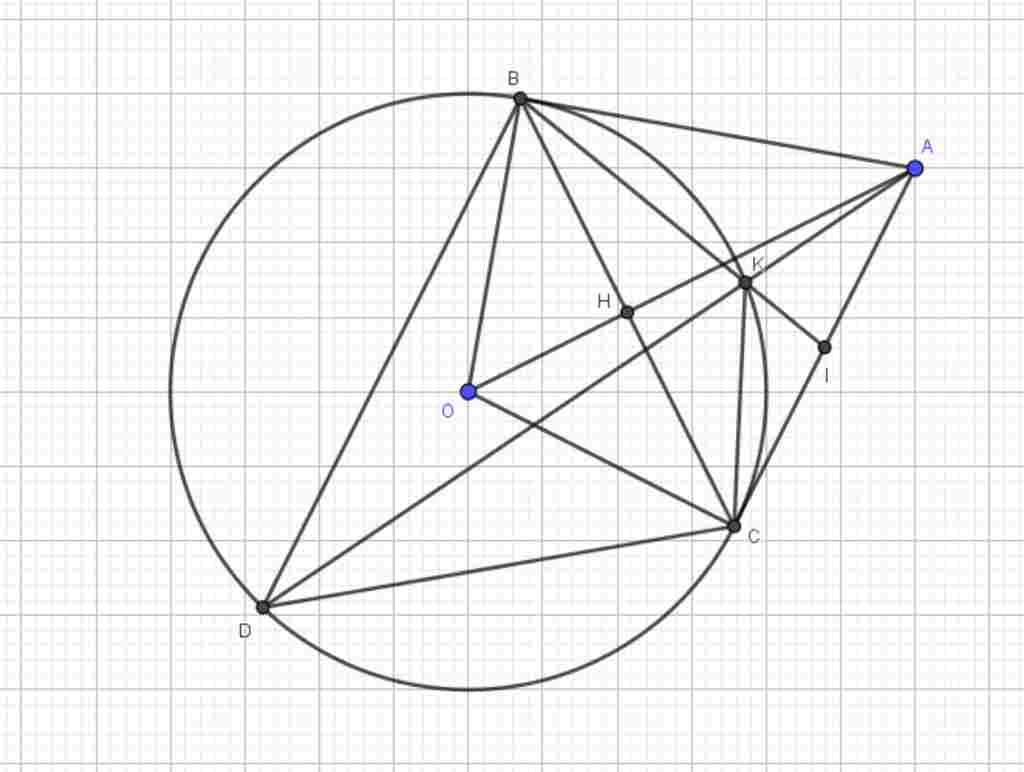
Giúp em bài tập về nhà Toán lớp 9 câu hỏi như sau: Cho đường tròn tâm O, bán kính R. Từ điểm A bên ngoài đường tròn, kẻ 2
tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm). Từ B, kẻ đường thẳng song song
với AC cắt đường tròn tại D (D khác B). Nối AD cắt đường tròn (O) tại điểm thứ hai là K.
Nối BK cắt AC tại I.
a) Chứng minh tứ giác ABOC nội tiếp đường tròn.
b) Chứng minh rằng : IC^2=IK.IB
c) Cho góc BAC=60, chứng minh 3 điểm A, O, D thẳng hàng
Trả lời 1:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
a) Ta có: $AB, \, AC$ là các tiếp tuyến của $(O)$ tại $A, \, B \, (gt)$
$\Rightarrow OB\perp AB; \, OC\perp AC$
$\Rightarrow \widehat{OBA} = \widehat{OCA}= 90^o$
Xét tứ giác $ABOC$ có:
$\widehat{OBA} + \widehat{OCA} = 180^o$
Do đó $ABOC$ là tức giác nội tiếp
b) Xét $ΔIKC$ và $ΔICB$ có:
$\widehat{I}:$ góc chung
$\widehat{ICK} = \widehat{IBC}$ (cùng chắn $\overparen{CK}$)
Do đó $ΔIKC\sim ΔICB \, (g.g)$
$\Rightarrow \dfrac{IK}{IC} = \dfrac{IC}{IB}$
$\Rightarrow IC^2 = IK.IB$
c) Ta có: $AB = AC$
$\Rightarrow ΔABC$ cân tại $A$
mà $\widehat{BAC} = 60^o$
$\Rightarrow ΔABC$ đều
$\Rightarrow \overparen{BC} = 120^o$
$\Rightarrow \widehat{BDC} = 60^o$ (góc nội tiếp chắn $\overparen{BC}$)
Ta lại có: $\widehat{DBC} = \widehat{BCA}$ (so le trong)
$\Rightarrow \widehat{DBC} = 60^o$
$\Rightarrow ΔDBC$ đều
$\Rightarrow \widehat{DOB} = 120^o$
mà $\widehat{BOA} = \dfrac{\overparen{BC}}{2} = 60^o$
$\Rightarrow \widehat{DOB} + \widehat{BOA} = 180^o$
$\Rightarrow A, O, D$ thẳng hàng