Câu hỏi:
Giúp em bài tập về nhà Toán lớp 9 câu hỏi như sau: định lý Menelaus là j? chứng minh định lý ấy
Trả lời 2:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
Giải đáp:
Dưới
Lời giải và giải thích chi tiết:
Cho $Δ_{ABC}$.$D, E, F$ lần lượt nằm trên các đường thẳng $BC, CA, AB$. Khi đó định lý phát biểu rằng $D, E, F$ thẳng hàng khi và chỉ khi $\dfrac{FA}{FB}×\dfrac{DB}{DC} . \dfrac{EC}{EA} = 1$
$CM$:Hình$↓$
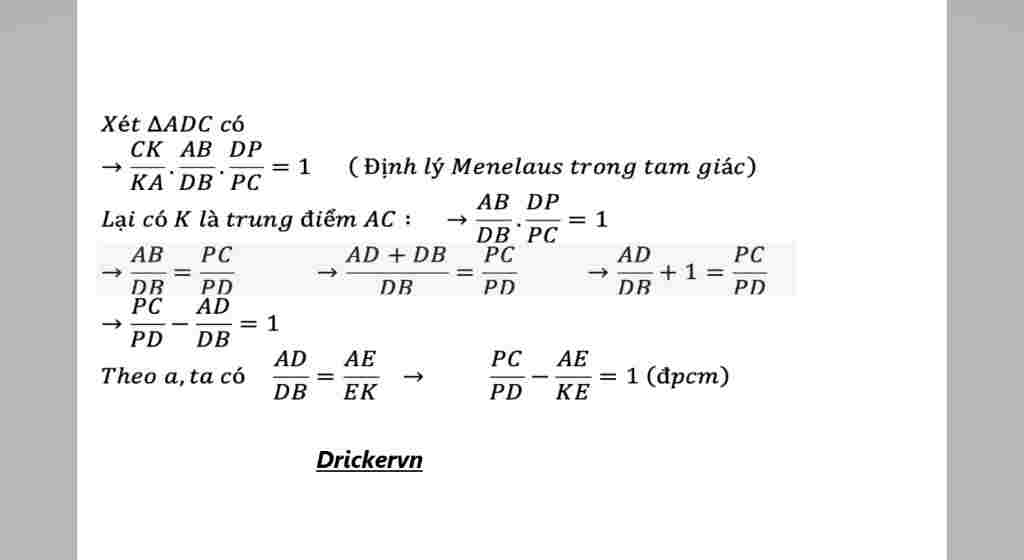
Trả lời 1:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
Lời giải và giải thích chi tiết:
Định lý Menelaus là một định lý cơ bản trong hình học tam giác, được phát biểu như sau: Cho tam giác ABC. Các điểm D, E, F lần lượt nằm trên các đường thẳng BC, CA, AB. Khi đó D, E, F thẳng hàng khi và chỉ khi :
FA/FB . DB/DC . EC/EA = 1 . Bn thông cảm mk ko viết đúng đc.Có gì bn xem trong sgk ý
Chứng minh :
VD về định lí Menelaus thuận : Cho tam giác ABC. Trên BC,CA,AB lần lượt lấy các điểm D,E,F sao cho chúng thẳng hàng. CMR : FA/FB . DB/DC . EC/EA = 1
Ta kẻ CG//AB (g ∈ DE)
DB/DC = FB/CG , EC/EA = CG/FA
⇒ DB/DC . EC/EA = FB/FA ⇔ DB/DC . EC/EA . FA/FB = 1
VD về định lí Menelaus đảo: Cho tam giác ABC. Trên BC,CA,AB lần lượt lấy các điểm D,E,F sao cho FA/FB . DB/DC . EC/EA = 1. CMR D,E,F thẳng hàng.
Lấy F’ là giao của AB và DE
Ta CMR : F’≡F
Ta có : DB/DC . EC/EA . F’A/F’B=1
⇒ F’A/F’B = FA/FB ⇔ F’A/FA = F’B/FB = F’A+F’B/FA+FB = 1
⇒ F’ ≡ F






