Câu hỏi:
Giúp em bài tập về nhà Toán lớp 9 câu hỏi như sau: Cho đường tròn (O) và cát tuyến CAB (C ở ngoài đường tròn), từ điểm chính giữa của cung lớn AB kẻ đường kính MN cắt AB tại I, CM cắt đường tròn tại E, EN cắt đường thẳng AB tại F.
a. Ch.m MEFI là tứ giác nội tiếp
b. Ch.m góc CEA = góc MEB
c. Ch.m CE.CM=CF.CI=CA.CB
Trả lời 2:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
Đây nha bn ????
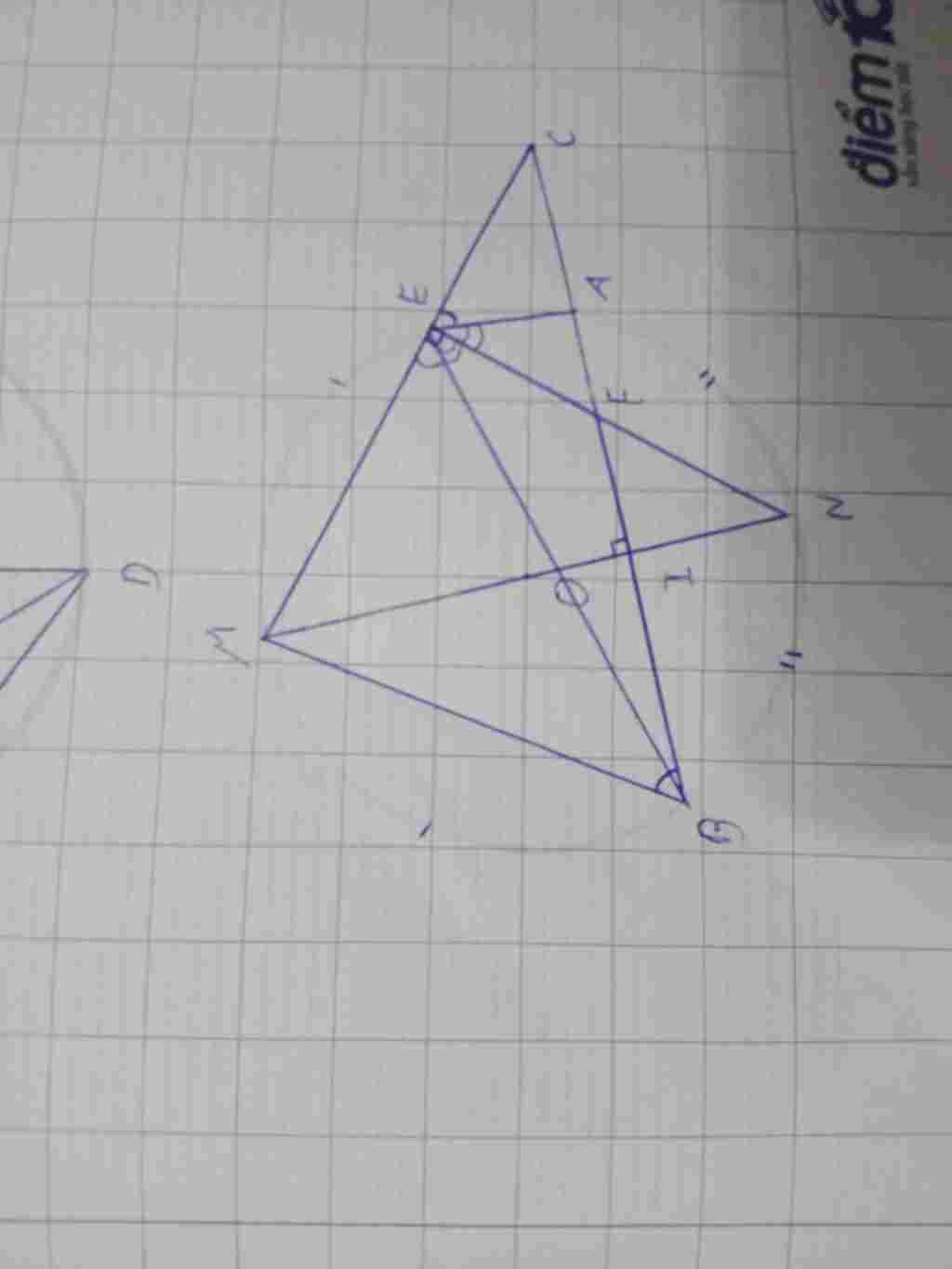
Trả lời 1:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
a) Do $M$ là điểm chính giữa $\overparen{AB}$ lớn
⇒ $N$ là điểm chính giữa $\overparen{AB}$ nhỏ
⇒ $MN\perp AB$
⇒ $\widehat{MIA} = 90^o$ hay $\widehat{MIF} = 90^o$
Bên cạnh đó, $\widehat{MEN} = 90^o$ (nhìn đường kính $MN$)
hay $\widehat{MEF} = 90^o$
Xét tứ giác $MEFI$ có:
$\widehat{MIF} + \widehat{MEF} = 180^o$
Do đó $MEFI$ là tứ giác nội tiếp
b) Ta có: $MEAB$ là tứ giác nội tiếp (4 điểm $M,E,A,B$ cùng thuộc $(O)$)
⇒ $\widehat{CEA} = \widehat{MBA}$ (cùng bù $\widehat{MEA}$)
mà $\widehat{MBA} = \widehat{MEB}$ $(\overparen{MB} = \overparen{MA})$
nên $\widehat{CEA} = \widehat{MEB}$
c) Xét $ΔCEA$ và $ΔCBM$ có:
$\widehat{MCB}:$ góc chung
$\widehat{CEA} = \widehat{CBM}$ (cùng bù $\widehat{MEA}$)
Do đó $ΔCEA\sim ΔCBM \, (g.g)$
⇒ $\dfrac{CE}{CB}= \dfrac{CA}{CM}$
hay $CE.CM = CA.CB$ $(1)$
Xét $ΔCEF$ và $ΔCIM$ có:
$\widehat{MCI}:$ góc chung
$\widehat{CIM} = \widehat{CEF} = 90^o$
Do đó $ΔCEF\sim ΔCIM \, (g.g)$
⇒ $\dfrac{CE}{CI} = \dfrac{CF}{CM}$
hay $CE.CM = CI.CF$ $(2)$
Từ $(1)(2) ⇒ CE.CM = CF.CI = CA.CB$





