Câu hỏi:
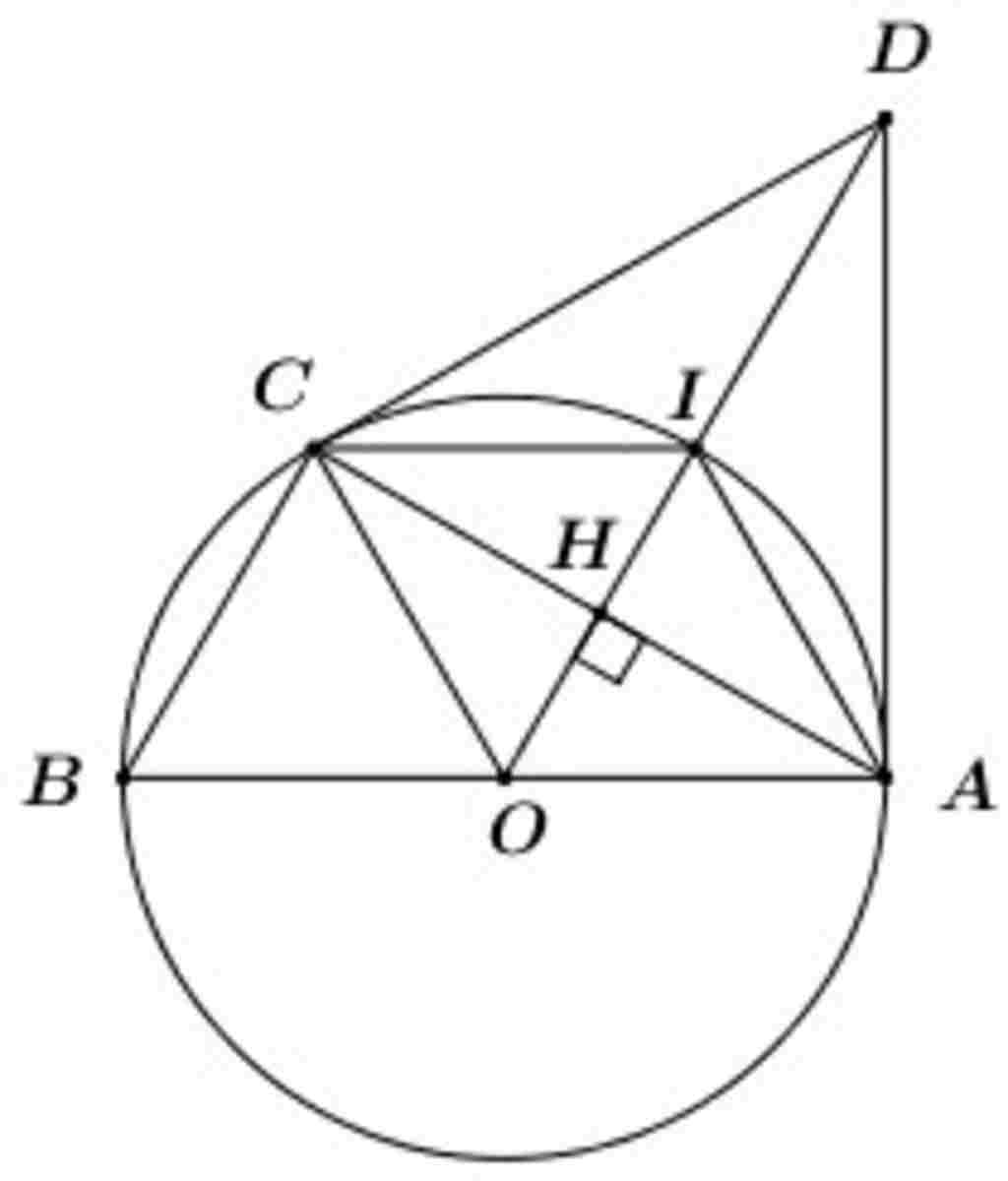
Giúp em bài tập về nhà Toán lớp 9 câu hỏi như sau: cho đường tròn (O;R), đường kính AB, dây cung BC=R
a) tính các cạch và các góc chưa biết của tam giác ABC theo R
b) đường thẳng qua O vuông góc với AC cắt tiếp tuyến tại A của đường tròn (O) tại D, chứng minh DC là tiếp tuyến của đường tròn (O)
c)đường thẳng OD cắt đường tròn (O) tại I. C/M I là tâm đường tròn nội tiếp tam giác ABC
ai giải giúp với
Trả lời 1:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
Giải đáp:
Bạn tham khảo nhé!
Lời giải và giải thích chi tiết:
a) \(\widehat {ACB} = {90^0}\) (góc nội tiếp chắn nửa đường tròn)
Áp dụng định lí Pytago trong tam giác vuông ABC ta có:
\(\begin{array}{l}A{B^2} = A{C^2} + B{C^2}\\ \Rightarrow {\left( {2R} \right)^2} = A{C^2} + {R^2}\\ \Rightarrow A{C^2} = 3{R^2}\\ \Rightarrow AC = R\sqrt 3 \end{array}\)
Ta có:
\(\begin{array}{l}\sin A = \frac{{BC}}{{AB}} = \frac{R}{{2R}} = \frac{1}{2} \Rightarrow \widehat A = {30^0}\\ \Rightarrow \widehat B = {90^0} – \widehat A = {60^0}\end{array}\)
b) Gọi \(H = OD \cap AC\) ta có:
\(OD \bot AC\) tại H \( \Rightarrow H\) là trung điểm của AC
\( \Rightarrow OD\) là trung trực của AC
\( \Rightarrow DA = DC\) (tính chất đường trung trực).
Xét \(\Delta OAD\) và \(\Delta OCD\) có:
\(\begin{array}{l}OA = OC\,\left( { = R} \right)\\OD\,\,chung\\DA = DC\,\,\left( {cmt} \right)\\ \Rightarrow \Delta OAD = \Delta OCD\,\,\left( {c.c.c} \right)\end{array}\)
\( \Rightarrow \widehat {OAD} = \widehat {OCD}\) (hai góc tương ứng).
Mà \(\widehat {OAD} = {90^0}\,\,\left( {gt} \right) \Rightarrow \widehat {OCD} = {90^0}\)
\( \Rightarrow OC \bot CD \Rightarrow CD\) là tiếp tuyến của đường tròn (O) tại C.
c) Tam giác ACD có DA = DC \( \Rightarrow \Delta ACD\) cân tại D.
\( \Rightarrow \) Trung trực OH đồng thời là phân giác.
Tam giác OBC đều \( \Rightarrow \widehat {BOC} = {60^0} \Rightarrow \widehat {AOC} = {120^0}\).
Áp dụng tính chất 2 tiếp tuyến cắt nhau ta có \(OD\) là phân giác của \(\widehat {AOC}\).
\( \Rightarrow \widehat {AOD} = \widehat {COD} = {60^0}\)
\( \Rightarrow \Delta OAI\) đều \(\left( {OA = OI,\,\,\widehat {OAI} = {{60}^0}} \right) \Rightarrow \widehat {OAI} = {60^0}\) và đường cao AH đồng thời là phân giác của \(\widehat {OAI}\) .
\( \Rightarrow \widehat {OAH} = \widehat {IAH} = {30^0}\).
Lại có \(\widehat {IAD} = {90^0} – \widehat {OAI} = {90^0} – {60^0} = {30^0}\).
\( \Rightarrow \widehat {IAH} = \widehat {IAD} \Rightarrow IA\) là phân giác của \(\widehat {HAD}\).
Mà \(DH \cap IA = I \Rightarrow I\) là tâm đường tròn nội tiếp tam giác ACD.