Câu hỏi:
Giúp em bài tập về nhà Toán lớp 8 câu hỏi như sau: Cho tam giác ABC có 3 góc nhọn và
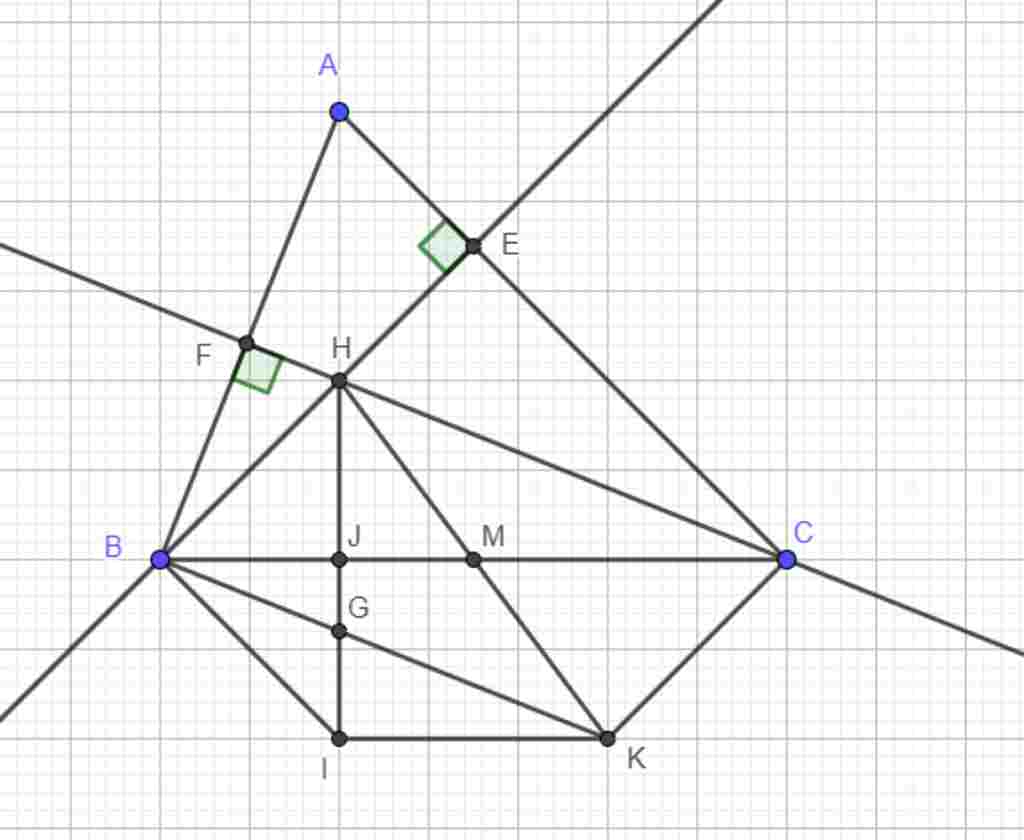
AB <AC. Các đường cao BE, CF cắt nhau tại H. Gọi M là trung điểm của BC. Trên tia đối của MH lấy điểm K sao cho HM =MK
a) Chứng minh : Tứ giác BHCK là hình bình hành
b) Chứng minh BK vuông góc AB và CK vuông góc AC
c) Gọi I là điểm đối xứng với H qua BC. Chứng minh : Tứ giác BIKC là hình thang cân
d) BK cắt HI tại G. Tam giác ABC phải có thjêm điều kiện gì để tứ giác GHCK là hình thang cân
Trả lời 2:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
Xin hay nhất cho nhóm.

Trả lời 1:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
a) Tứ giác $BHCK$ có 2 đường chéo $HK$ và $BC$ cắt nhau tại trung điểm $M$ của mỗi đường
Do đó tứ giác $BHCK$ là hình bình hành
b) Tứ giác $BHCK$ là hình bình hành
$\Rightarrow BK\parallel CH$
Mà $CH\bot AB$
$\Rightarrow BK\bot AB$ (đpcm)
c) Gọi $J=BC\cap HI$
Xét $\Delta BHI$ có $BJ$ vừa là đường trung tuyến, vừa là đường cao nên $\Delta BHI$ cân đỉnh B
$\Rightarrow BJ$ là đường phân giác của $\widehat{HBI}$
$\Rightarrow \widehat{IBC}=\widehat{HBC}$
mà $\widehat{HBC}=\widehat{KCB}$ (hai góc ở vị trí so le trong do BH//CK)
Từ 2 điều trên $\Rightarrow\widehat{IBC}=\widehat{KCB}$ (*)
$\Delta HIK$ có $JM$ là đường trung bình của tam giác, nên $JM//IK$
Hay $BC//IK\Rightarrow BIKC$ là hình thang (**)
Từ (*) và (**) suy ra $BIKC$ là hình thang cân.
d) Tứ giác $GHCK$ có $GK\parallel HC$
Do đó $GHCK$ là hình thang
Để $GHCK$ là hình thang cân thì $\widehat{GHC}=\widehat{KCH}$
mà $\widehat{KCH}=\widehat{HBK}$ (hai góc cùng bù $\widehat{BHC}$ do $BHCK$ là hình bình hành)
Từ hai điều trên $\Rightarrow\widehat{GHC}=\widehat{HBK}$
$\Delta HJC:\widehat{HCJ}=90^o-\widehat{GHC}$ (tổng ba góc trong tam giác bằng $180^o$)
$\widehat{ABH}=\widehat{ABK}-\widehat{HBK}=90^o-\widehat{HBK}$ ($BK\bot AB$)
Từ 3 điều trên suy ra $\widehat{HCJ}=\widehat{ABH}$
Mà $\Delta BCF:\widehat{FBC}=90^o-\widehat{HCJ}$
$\Delta ABE:\widehat{EAB}=90^o-\widehat{ABH}$
Từ 3 điều trên $\Rightarrow\widehat{FBC}=\widehat{EAB}$
hay $\widehat{CBA}=\widehat{CAB}$
$\Rightarrow \Delta ABC$ cân đỉnh $C$
$\Delta ABC$ cân đỉnh $C $ thì $GHCK$ là hình thang cân.