Câu hỏi:
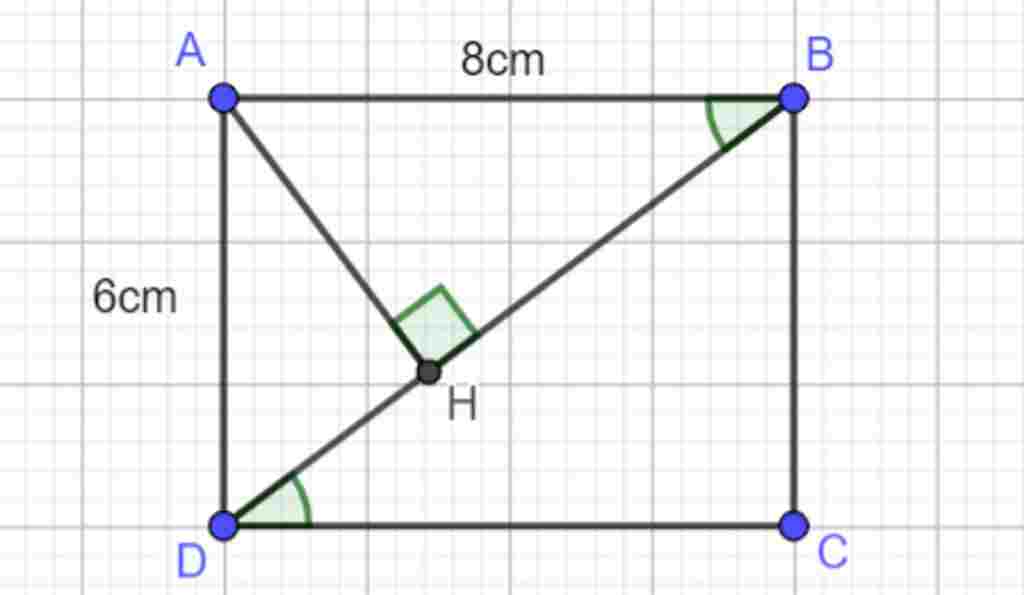
Giúp em bài tập về nhà Toán lớp 8 câu hỏi như sau: Bài 1: Cho hình chữ nhật ABCD có AB = 8cm, BC = 6cm. Vẽ đường cao AH của tam giác
ADB.
a) Chứng minh: tam giác AHB đồng dạng tam giác BCD
b) Chứng minh: AD^2 = DH .DB
c) Tính độ dài đoạn thẳng DH, AH.
Trả lời 2:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
Hình bạn tự vẽ nha.
Lời giải và giải thích chi tiết:
Hình bạn tự vẽ nha!
a)Xét tam giác HBA và tam giác ABD có:
góc AHB=góc DAB(=90độ)
góc B chung
=> tam giác HBA đồng dạng tam giác ABD (g-g)
b) xét tam giác HDA và tam giác ADB có
góc AHD =góc DAB(=90độ)
góc D chung
=> tam giác HDA đồng dạng tam giác ADB (g-g)
=>AD/BD=HD/BD=>AD^2=DH.BD
c)vì ABCD là hcn=> BC=AD=6cm
tam giác ABD vuông tại A=> BD^2=AD^2+AB^2(ĐL Pytago)
=>BD^2=6^2+8^2
=>BD=10(cm)
Có AD^2=DH.BD=>6^2=DH.10=>DH=3.6(cm)
tam giác ADH vuông tại H
=>Ad^2=AH^2+HD^2(ĐL Pytago)
=>6^2=AH^2+3,6^2
=>AH=4.8(cm)
Trả lời 1:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
a) Xét $\Delta AHB$ và $\Delta BCD$ có:
$\widehat{AHB}=\widehat{BCD}$ $(=90^o)$
$\widehat{ABH}=\widehat{BDC}$ (hai góc ở vị trí so le trong)
$\Rightarrow\Delta AHB\sim\Delta BCD$ (g.g)
b) Xét $\Delta DHA$ và $\Delta DAB$ có:
$\widehat D$ chung
$\widehat{DHA}=\widehat{DAB}$ $(=90^o)$
$\Rightarrow\Delta DHA\sim\Delta DAB$ (g.g)
$\Rightarrow \dfrac{AD}{BD}=\dfrac{DH}{DA}$ (hai cạnh tương ứng tỉ lệ)
$\Rightarrow AD^2=DH.BD$
c) Áp dụng định lý Pitago vào $\Delta ABD\bot A$ có:
$BD^2=AD^2+AB^2=100\Rightarrow BD=10cm$
Từ $AD^2=DH.BD$ chứng minh ở câu b suy ra
$DH=\dfrac{AD^2}{BD}=3,6cm$
$S_{ABD}=\dfrac{AH.BD}2=\dfrac{AD.AB}2$
$\Rightarrow AH=\dfrac{AD.AB}{BD}=4,8cm$