Câu hỏi:
Giúp em bài tập về nhà Toán lớp 8 câu hỏi như sau:
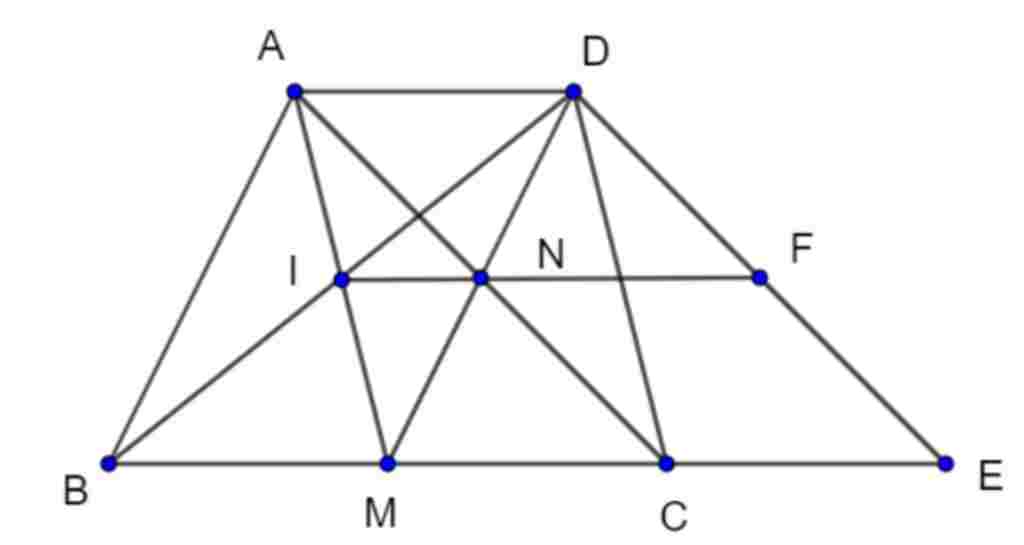
Cho tam giác ABC nhọn(AB < AC). Lấy điểm M, điểm N lần lượt là trung điểm của các cạnh BC
và AC. Lấy điểm D đối xứng với điểm M qua điểm N. Gọi điểm I là trung điểm của đoạn AM.
a) Tứ giác ADCM là hình gì? Vì sao?
b) Chứng minh B,I,D thẳng hàng.
c) Qua điểm D kẻ đường thẳng song song với AC, cắt đường thẳng BC tại điểm
Đường thẳng
IN cắt DE tại điểm F . Tìm điều
kiện của tam giác ABC để tứ giác MNFE là hình thang cần.
Trả lời 1:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
Giải đáp:
a) Hình bình hành
c) ΔABC cân tại A
Lời giải và giải thích chi tiết:
a) D đối xứng với M qua N
=> N là trung điểm của MD
Xét tứ giác ADCM có:
N là trung điểm của AC
N là trung điểm của MD
=> ADCM là hình bình hành
b) ADCM là hình bình hành
=> $AD//MC; AD=MC$
M là trung điểm của BC => M∈BC; MC=MB
=> $AD//MB; AD=MB$
=> ADMB là hình bình hành
mà I là trung điểm của AM
=> I là trung điểm của BD
=> B, I, D thẳng hàng
c) Xét ΔAMD có:
I, N lần lượt là trung điểm của AM, MD
=> IN là đường trung bình
=> $IN//AD$
mà $AD//MC$ => $IN//MC$
lại có F∈IN; E∈MC => $NF//ME$
=> MNFE là hình thang
Để MNFE là hình thang cân
=> \hat{E}=\hat{NMC} (1)
$DE//AC$ => \hat{E}=\hat{ACB} (2 góc đồng vị) (2)
ADMB là hình bình hành => $AB//MD$
=> \hat{ABC}=\hat{NMC} (2 góc đồng vị) (3)
Từ (1) (2) (3) => \hat{ABC}=\hat{ACB}
=> ΔABC cân tại A
Vậy ΔABC cân tại A thì MNFE là hình thang cân