Câu hỏi:
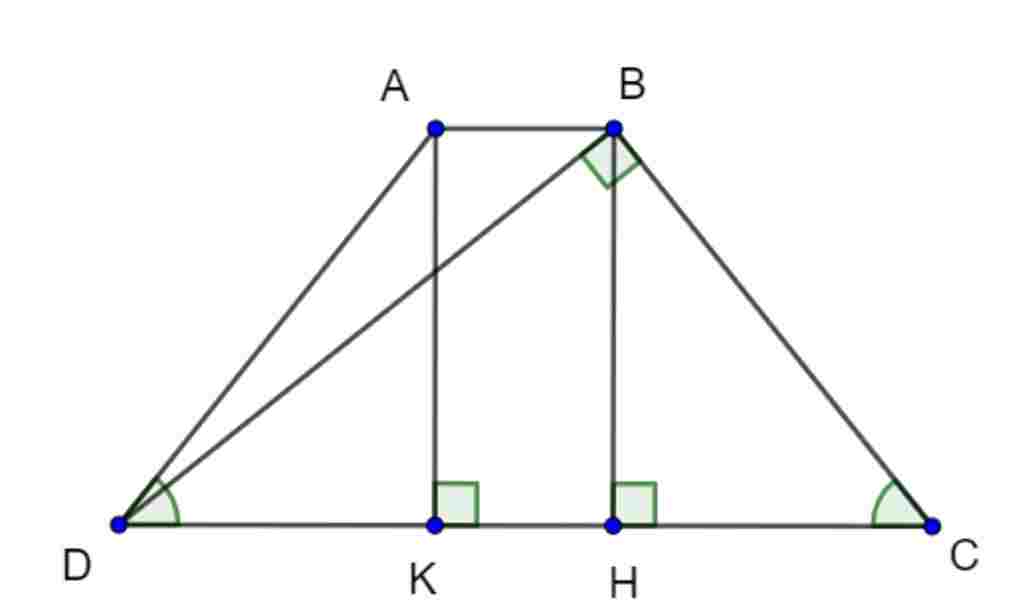
Giúp em bài tập về nhà Toán lớp 8 câu hỏi như sau: Bài 3: Cho hình thanh cân ABCD có AB II DC và AB< DC, đường chéo BD
vuông góc với cạnh bên BC. Vẽ đường cao BH, AK.
a) Chứng minh - BDC s HBC b) Chứng minh BC? = HC.DC
c) Chứng minh AKD BHC. d) Cho BC = 15cm, DC = 25 cm. Tính HC ,
HD .e) Tính diện tích hình thang ABCD.
Giúp e vs e vote 5 sao nha e camon ạ????????
Trả lời 2:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
a, Xét ΔBDC và ΔHBC:
góc DBC = góc BHC (=90 độ) (gt)
góc C chung
=> ΔBDC ~ ΔHBC (g.g)
b, Vì ΔBDC ~ ΔHBC (câu a)
=> BC/HC = DC/BC
=> BC^2 = HC.DC
c, Xét ΔADK và ΔBCH:
góc AKD = góc BHC ( =90 dộ)
góc ADK = góc BCH (Vì ABCD hình thang cân) (gt)
=> ΔADK ~ ΔBCH (g.g)
d, Có BC^2 = HC.DC (câu b)
=> 15^2 = 25.HC
=> HC = 9 (cm)
=> DH = DC – HC = 25 – 9 = 16 (cm)
d, Xét ΔBHC: góc BHC = 90 độ (gt)
=> BC^2 = HC^2 + BH^2 (Pytago)
=> 15^2 = 9^2 + BH^2
=> BH^2 = 144
=> BH = 12 (cm)
Có ΔADK ~ ΔBCH (câu c)
Mà AD = BC (Vì ABCD hình thang cân)
=> ΔADK = ΔBCH
=> DK = CH
=> DK + CH = DC – KH
=> KH = DC – 2CH =25 – 2.9 = 7 (cm)
Tứ giác ABHK có: AK = BH
góc AKH = góc BHK (=90 độ)
=> ABHK là hình chữ nhật
=> AB = KB
=> AB = 7 (cm)
e, Diện tích hình thang cân ABCD: SABCD = 1/2.AK(AB + DC) = 1/2.12.(7 + 25) = 192 (cm^2)
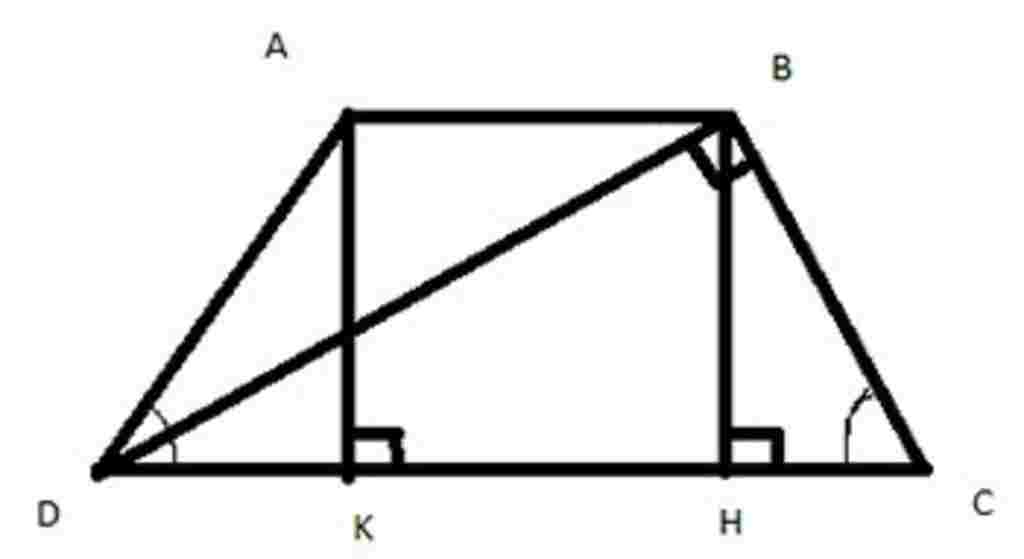
Trả lời 1:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
Lời giải và giải thích chi tiết:
a) BH, AK là đường cao của hình thang ABCD
=> BH⊥CD; AK⊥CD
Xét ΔBDC và ΔHBC có:
\hat{DBC}=\hat{BHC}=90^0 (DB⊥BC; BH⊥CD)
\hat{BCD}: chung
=> $ΔBDC\backsimΔHBC$ (g.g)
b) $ΔBDC\backsimΔHBC$
=> \frac{BC}{HC}=\frac{DC}{BC} (tỉ số đồng dạng)
=> BC^2=HC.DC
c) ABCD là hình thang cân
=> \hat{ADC}=\hat{BCD} hay \hat{ADK}=\hat{BCH}
Xét ΔAKD và ΔBHC có:
\hat{AKD}=\hat{BHC} (AK⊥CD; BH⊥CD)
\hat{ADK}=\hat{BCH}
=> $ΔAKD\backsimΔBHC$ (g.g)
d) Vì BC^2=HC.DC
=> 15^2 = HC . 25
=> HC=9cm
DC=HD+HC => HD=DC-HC=25-9=16cm
e) $ΔAKD\backsimΔBHC$ => \frac{AD}{BC}=\frac{KD}{HC}
mà AD=BC => \frac{KD}{HC}=1 => KD=HC=9cm
BH⊥CD => ΔBHC vuông tại H
=> BC^2=BH^2+HC^2 (định lý pytago)
=> 15^2=BH^2 + 9^2
=> BH^2=144 => BH=12cm
HD=HK+KD => HK=HD-KD=16-9=7cm
AK⊥CD; BH⊥CD => $AK//BH$
mà $AB//HK$ (vì $AB//CD$) => ABHK là hình bình hành
=> AB=HK=7cm
Diện tích hình thang ABCD là:
1/2 (AB+CD) . BH = 1/2 . (7+25) . 12 = 192cm^2