Câu hỏi:
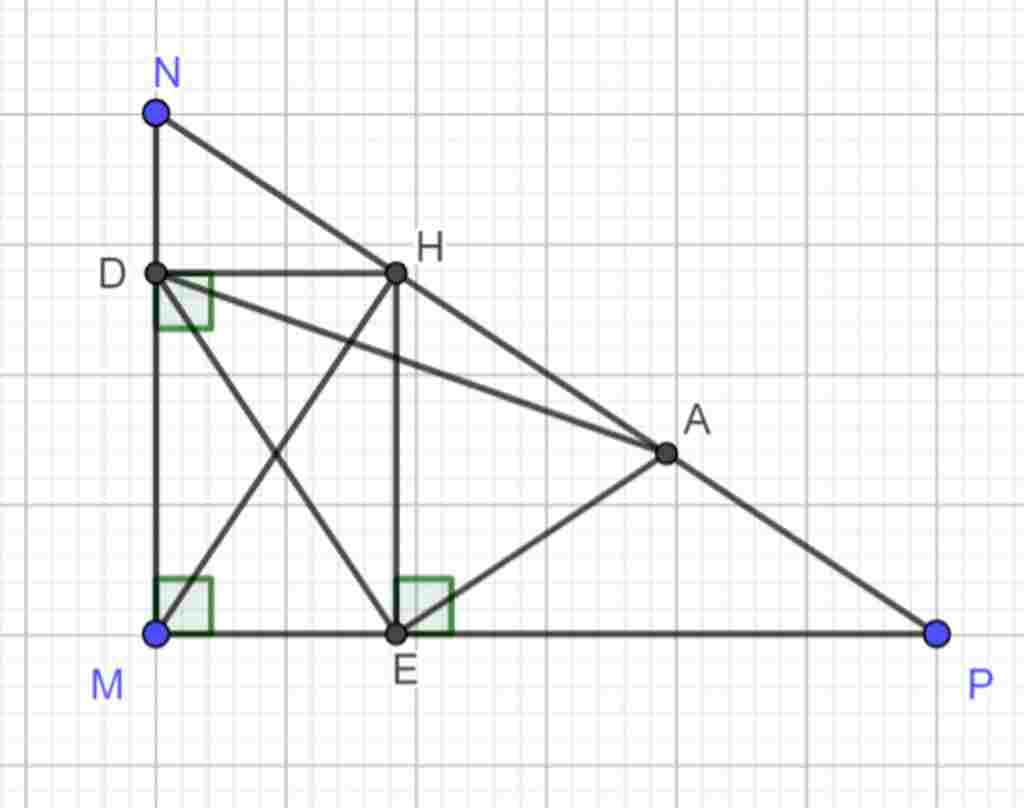
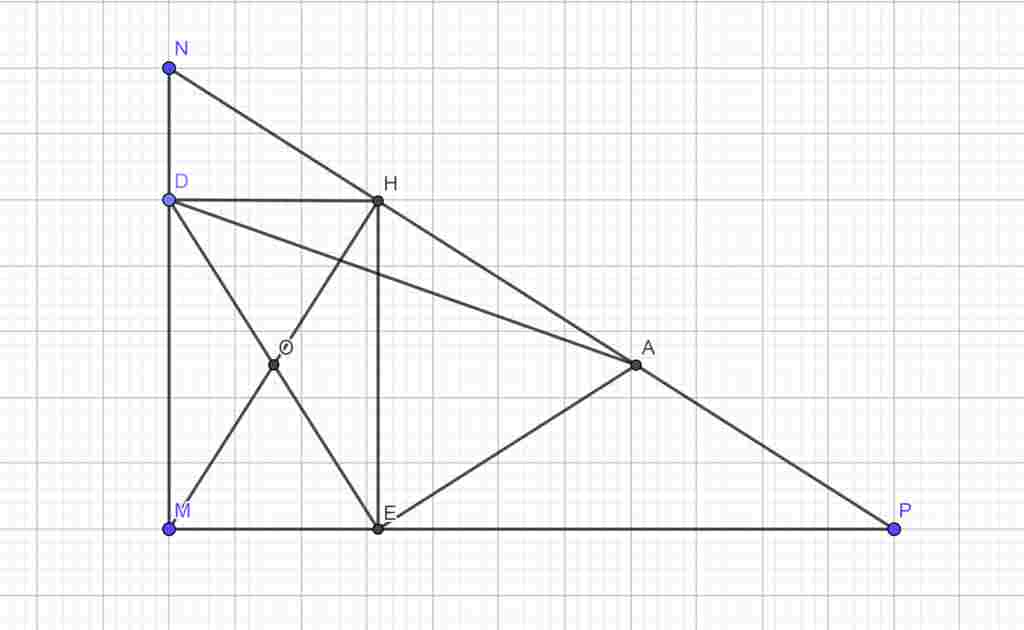
Giúp em bài tập về nhà Toán lớp 8 câu hỏi như sau: Cho tam giác MNP vuông tại M đường cao MH . Gọi D,F lần lượt là chân các đường vuông góc HA từ H xuống MN và MP
a/Chứng minh tứ giác MDHE là Hình Chữ Nhật
b/ Gọi A là trung điểm HP . Chứng minh ∆DEA vuông
c/ Tam giác MNP có thêm điều kiện gì để DE=2EA
Trả lời 2:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
Lời giải và giải thích chi tiết:
a) Xét tứ giác MDHE có $\widehat{DME}=\widehat{ MDH}=\widehat{ MEH}=90^o$
=> Tứ giác MDHE là hình chữ nhật
b) Gọi $DE\cap MH = O$
Ta có tứ giác MDHE là hình chữ nhật
=> OH=OE
=> ΔOHE cân tại O
=> $\widehat{OHE}=\widehat{ OEH}$
Xét $ΔHEP\bot E$ có EA là trung tuyến
=> AE=AH
=>ΔAHE cân tại A
=> $\widehat{AHE}=\widehat{ AEH}$
=> $\widehat{AHE}+\widehat{ OHE}=\widehat{ AEH}+\widehat{ OEH}$
=> $\widehat{ AED}=\widehat{ AHM}=90^o$
=> $ΔDEA\bot E$
c) Ta có HP=2AE
=> DE=2EA
mà:
DE=MH
2AE=HP
<=> MH=HP<=> ΔHMP vuông cân tại H
=> $\widehat{ HPM}=45^o$
<=> $\widehat{ MNP}=45^o$
<=>ΔMNP vuông cân tại M
Vậy ΔMNP vuông cân tại M thì DE=2AE.
Trả lời 1:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
a) Tứ giác MDHE có ∠M=∠D=∠e=90∘
Vậy tứ giác MDHE là hình chữ nhật vì có 3 góc vuông.
b) Ta có: ∠DEH=∠MHE (do MDHE là hình chữ nhật)
∠HEA=∠EHA (dễ dàng chứng minh được △HEA cân tại A nhờ giả thiết A trung điểm HP và HE⊥MP)
Mà ∠MHE+∠EHA=90∘
nên ∠DEH+∠HEA=∠DEA=90∘
⇒ đ.p.c.m
c) Ta có: DE=MH
2EA=HP
Để DE=2EA thì MH=HP
⇔ Tam giác MHP cân tại H
⇔ Tam giác MHP vuông cân tại H
⇔ ∠P=45∘
⇔ Tam giác MNP vuông cân tại M.