Câu hỏi:
Giúp em bài tập về nhà Toán lớp 8 câu hỏi như sau: Cho tam giác ABC, gọi D là điểm đối xứng với A qua B, E là điểm đối xứng với B qua C và F là điểm đối xứng với C qua A. Chứng minh rằng: ΔABC, ΔDEF có cùng trọng tâm
(giúp với ạ)
Trả lời 1:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
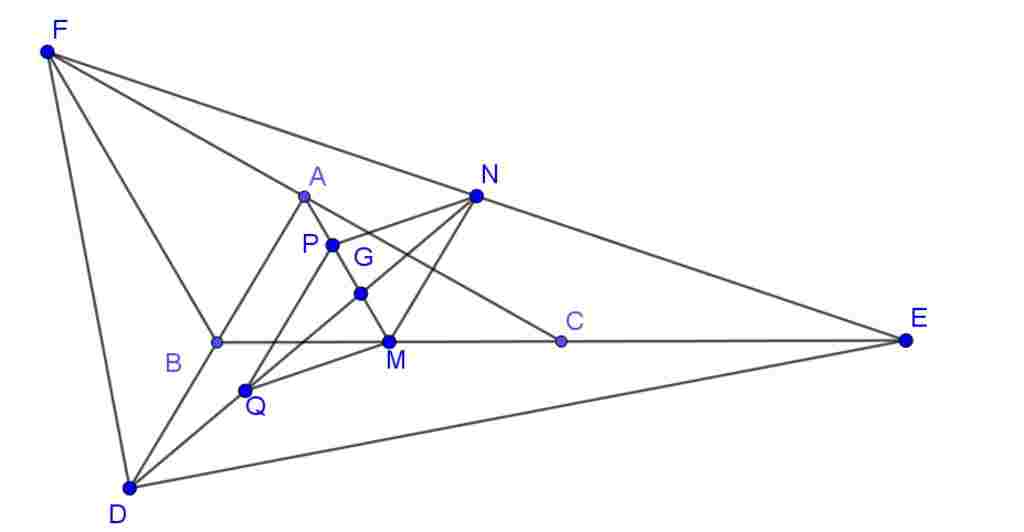
Gọi:
$M$ là trung điểm $BC$
$N$ là trung điểm $EF$
$G$ là giao điểm $BC$ và $EF$
$P$ là trung điểm $AG$
$Q$ là trung điểm $DG$
Mình gợi ý cách làm như sau:
$AN$ là đường trung bình $\Delta FCE$
$\to AN=\frac{1}{2}CE$ và $AN\,\,||\,\,CE$
$\to AN=\frac{1}{2}BC$ và $AN\,\,||\,\,BC$
$\to AN=BM$ và $AN\,\,||\,\,BM$
$\to ANMB$ là hình bình hành
$\to MN=AB$ và $MN\,\,||\,\,AB$
Mặt khác:
$PQ$ là đường trung bình $\Delta AGD$
$\to PQ=\frac{1}{2}AB$ và $PQ//AD$
$\to PQ=AB$ và $PQ\,\,||\,\,AB$
Vậy $MN=PQ$ và $MN\,\,||\,\,PQ$
$\to MNPQ$ là hình bình hành
Mà $G$ là giao điểm hai đường chéo $PM$ và $QN$
Nên $G$ là trung điểm $PM$ và $G$ là trung điểm $QN$
$\to PG=GM$ và $QG=GN$
Mặt khác:
$P$ là trung điểm $AG$ và $Q$ là trung điểm $DG$
$\to AP=PG$ và $DQ=QG$
Vậy $AP=PG=GM$ và $DQ=QG=DN$
$\to AG=\frac{2}{3}AM$ và $DG=\frac{2}{3}DN$
$\Delta ABC$ có $AM$ là đường trung tuyến
Mà $AG=\frac{2}{3}AM$
Nên $G$ là trọng tâm $\Delta ABC$
$\Delta DEF$ có $DN$ là đường trung tuyến
Mà $DG=\frac{2}{3}DN$
Nên $G$ là trọng tâm $\Delta DEF$
Vậy $\Delta ABC$ và $\Delta DEF$ có cùng trọng tâm $G$