Câu hỏi:
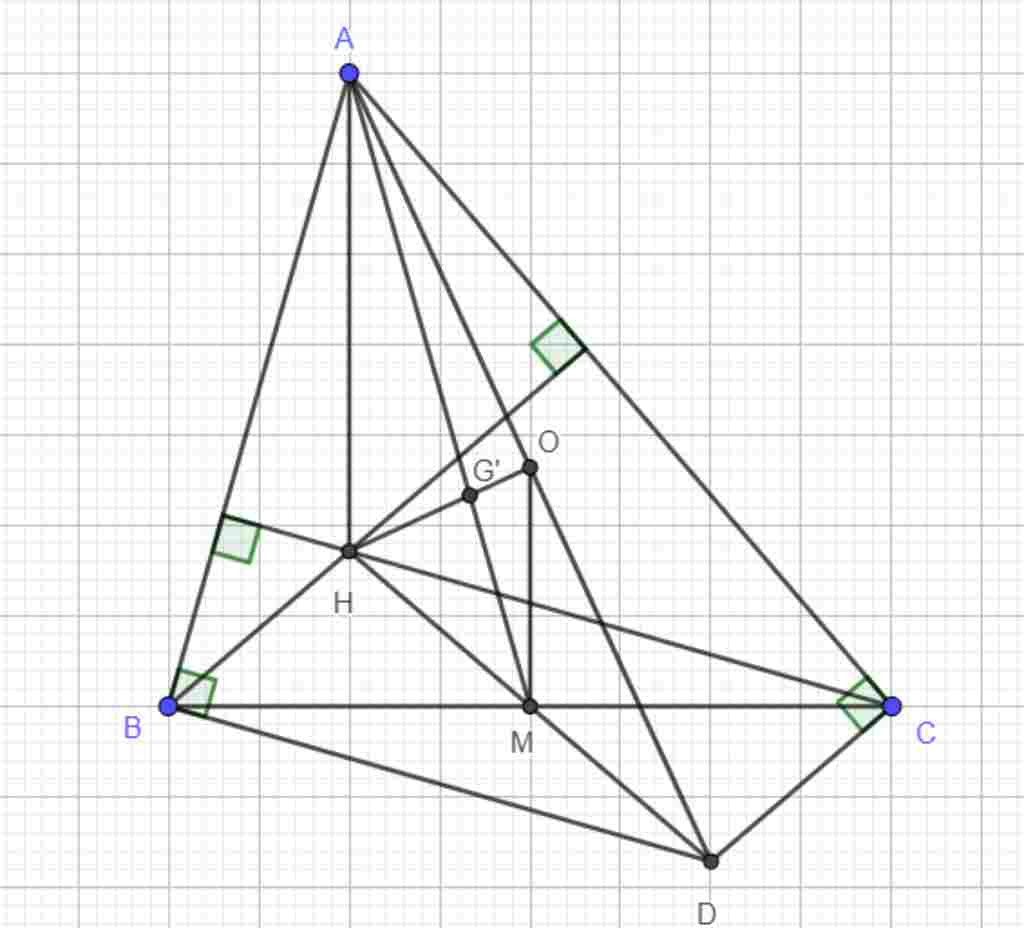
Giúp em bài tập về nhà Toán lớp 8 câu hỏi như sau: Cho tam giác ABC có ba góc nhọn, trực tâm H. Đường thẳng vuông góc với AB kẻ từ B cắt đường thẳng vuông góc với AC kẻ từ C tại D .
a) chứng minh tứ giác BHCD là hình bình hành
b) Gọi M là trung điểm BC , O là trung điểm AD . Chứng minh 2OM=AH
c) Gọi G là trọng tâm tam giác ABC . Chứng minh ba điểm H,G,O thẳng hàng .
Trả lời 2:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
a )
H là trực tâm của tam giác ABC => BH vuông góc với AC
Mà DC lạ vuông góc với AC(gt)
=> BH song song DC (1)
H là trực tâm của tam giác ABC => CH vuông góc với AB
Mà DB lạ vuông góc với AB(gt)
=> CH song song DB (2)
Từ (1) và (2) => Tứ giác BHCD có CH song song với DB; BH song song với CD
=> BHCD là hình bình hành.
b ) BHCD là hình bình hành nên đường chéo cắt nhau tại trung điểm mỗi đường
=> M cũng là trung điểm của HD
mà O là trung điểm của AD
=> OM là đường trung bình tam giác ADH
=> OM = 1/2AH (dpcm)
Cho mình 5 sao nha
Trả lời 1:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
Lời giải và giải thích chi tiết:
a. Ta có:
$\begin{cases}BH//DC(\perp AC)\\ CH//BD(\perp AB)\end{cases}$
$\rightarrow\Diamond BHCD\text{ là hình bình hành}$
b. Vì $\Diamond BHCD$ là hình bình hành
$\rightarrow BC\cap DH=M$ là trung điểm mỗi đường
Do O là trung điểm AD, M là trung điểm DH
$\rightarrow $OM là đường trung bình $\Delta AHD$
$\rightarrow OM=\dfrac{1}{2}AH\rightarrow 2OM=AH\rightarrow đpcm$
c. Gọi $AM\cap OH=G’$
Ta có $OM// AH$ (do OM là đương trung bình của $\Delta AHD$)
$\rightarrow \dfrac{MG’}{G’A}=\dfrac{OM}{AH}=\dfrac{1}{2}$
$\rightarrow $G’ là trọng tâm $\Delta ABC$
$\rightarrow G’\equiv G$
$\rightarrow H,G,O$ thẳng hàng
$\rightarrow đcpm$