Câu hỏi:
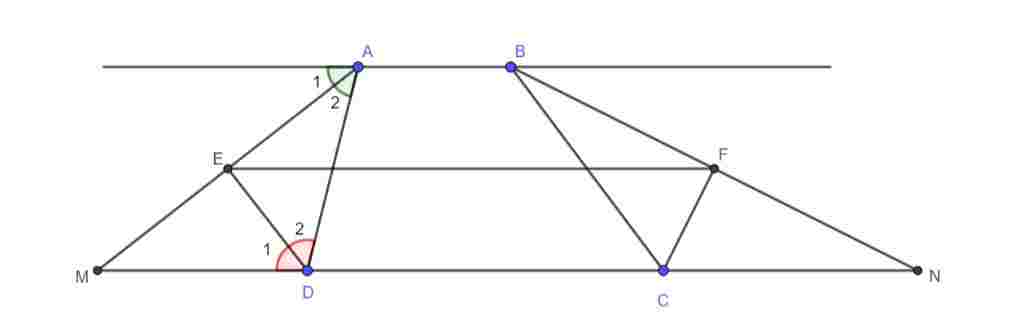
Giúp em bài tập về nhà Toán lớp 8 câu hỏi như sau: Cho hình thang ABCD (AB//CD). Các đường phân giác ngoài của góc A và D cắt nhau tại E, các đường phân giác ngoài của góc B và góc C cắt nhau tại F. Chứng minh:
a) EF song song với AB và CD.
b) EF có độ dài bằng nửa chu vi hình thang ABCD
Trả lời 1:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
CHO MÌNH CTLHN NHÉ !!!
a)
Vì $AE$ là phân giác góc ngoài của $\widehat A$ nên $\widehat{A_1}=\widehat{A_2}$
$DE$ là phân giác góc ngoài của $\widehat D$ nên $\widehat{D_1}=\widehat{D_2}$
Mà $\widehat{A_1}+\widehat{A_2}+\widehat{D_1}+\widehat{D_2}=180^o$ (hai góc ở vị trí trong cùng phía)
$\Rightarrow2\widehat{A_2}+2\widehat{D_2}=180^o$
$\Rightarrow\widehat{A_2}+\widehat{D_2}=90^o$
$\Rightarrow\Delta AED:\widehat{AED}=90^o$ (tính chất tổng 3 góc trong 1 tam giác)
$\Rightarrow DE\bot AE$
Gọi $AE\cap DC\equiv M$
$\Delta ADM$ có $DE$ vừa là đường cao vừa là đường phân giác nên $\Delta ADM$ cân đỉnh D
nên DE cũng là đường trung tuyến
$\Rightarrow E$ là trung điểm của AM
Gọi $BF\cap DC\equiv N$
Chứng minh tương tự có $F$ là trung điểm của BN
$\Rightarrow EF$ là đường trung bình của hình thang $ABNM$
$\Rightarrow EF//AB//CD$
b)
EF = (AB + MN)/2 (tính chất đường trung bình của hình thang)
=> EF = (AB + MD + CD + CN)/2 (1)
Mà MD = AD, CN = BC. Thay vào (1)
=> EF = (AB+AD+CD+BF)/2 (đpcm)