Câu hỏi:
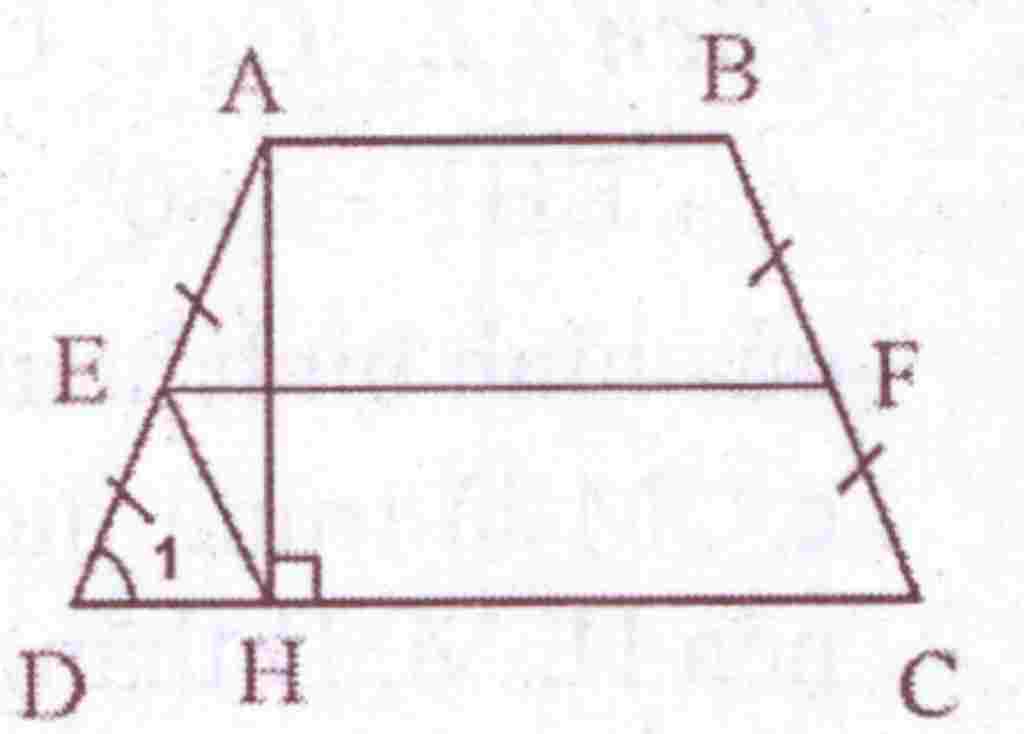
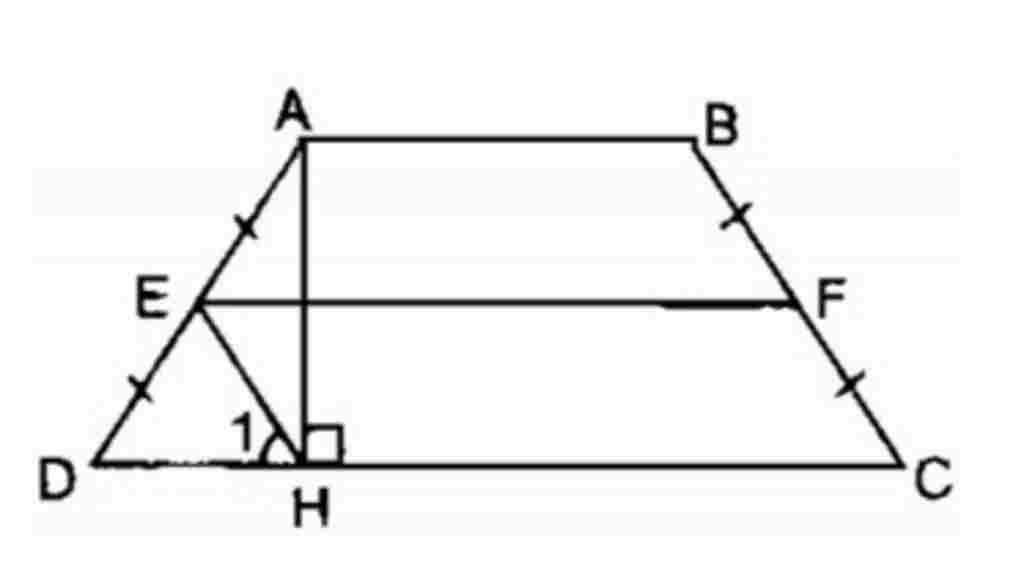
Giúp em bài tập về nhà Toán lớp 8 câu hỏi như sau: cho hình thang cân ABCD, đường cao AH. Gọi E,F lần lượt là trung điểm của các cạnh bên AD,BC.
Chứng minh rằng:EFCH là hình bình hành
Mong mọi người giúp mik vs!
Trả lời 2:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
Giải đáp: Ta có:
E là trung điểm của AD (gt)
F là trung điểm của BC (gt)
nên EF là đường trung bình của hình thang ABCD
⇒ EF // CD hay EF // CH
+)∆ AHD vuông tại H có HE là đường trung tuyến thuộc cạnh huyền AD.
Ta có: HE = ED = 1/2AD (tính chất tam giác vuông)
⇒ ∆ EDH cân tại E
góc D= góc H1 (tính chất tam giác cân)
(vì ABCD là hình thang cân)
Suy ra: góc H1
⇒ EH // CF (vì có cặp góc đồng vị bằng nhau)
Vậy tứ giác EFCH là hình bình hành.
Lời giải và giải thích chi tiết:
#Chúc bạn học tốt
#Mong được vote 5* và CTLHN
Trả lời 1:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
Giải đáp:
Tham khảo
Lời giải và giải thích chi tiết:
Vì ABCD là hình thang cân
$⇒AD=BC$
E,F lần lượt là trung điểm của AD,BC
⇒AE=ED=FC=$\frac{1}{2}$AD(1)
ΔADH vuông tại H
HE là trung tuyến
⇒ED=CH=$\frac{1}{2}$AD(2)
Từ (1) và (2)⇒EH=FC=$\frac{1}{2}$AD(3)
ΔDEA có ED=EH
⇒$\widehat{EDH}=\widehat{EHD}$
mà$\widehat{EDH}=\widehat{BCD}$ (do ABCD là hình thang cân)
⇒$\widehat{EHD}=\widehat{BCD}$
mà 2 góc vuông này ở vị trí so le trong
⇒$EH//FC$(4)
Từ(3) và (4)⇒EFCH là hình bình hành