Câu hỏi:
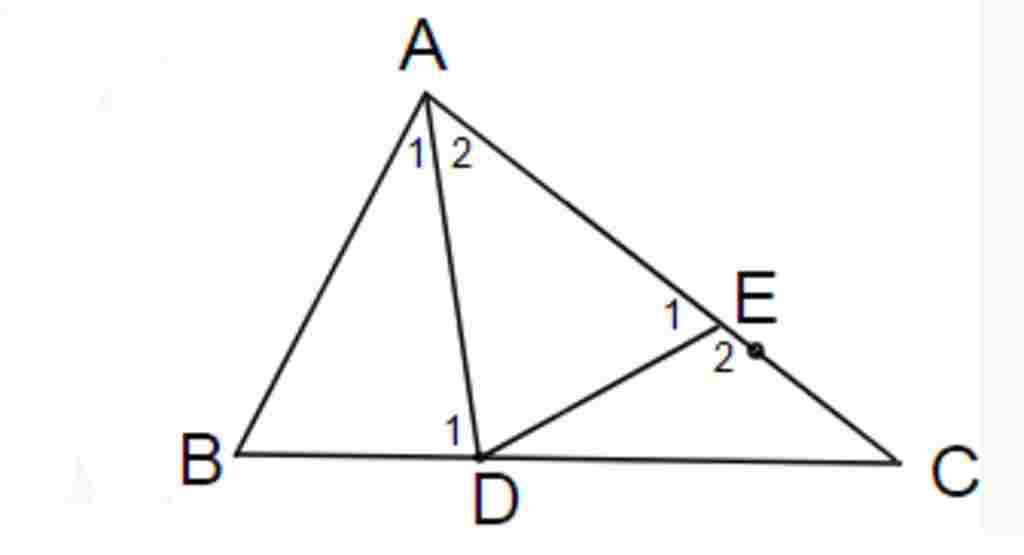
Giúp em bài tập về nhà Toán lớp 7 câu hỏi như sau: cho tam giác ABC có AB nhỏ hơn AC, AD là tia phân giác của góc A (D thuộc BC). Trên AC lấy điểm E sao cho AE =AB .a,so sánh: DC và DB. b,so sánh: góc ADB và góc ADC
Trả lời 2:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
Giải đáp:
Lời giải và giải thích chi tiết:
a) Xét △ABD và △ABE có:
AB = AD( gt)
∠A1=∠A2( vì AD là tia phân giác ∠BAC)
AD là cạnh chung
⇒△ABD = △ABE( c.g.c)
⇒∠B=∠E1( hai góc tương ứng) (1)
Áp dụng tính chất tổng ba góc cho △ABD
∠A1+∠D1+∠B=180o (2)
Ta có: ∠E1+∠E2=180o( Kề bù)(3)
Từ (2) và (3) ⇒ ∠A1+∠D1+∠B = ∠E1+∠E2(4)
Từ (4) và (1) ⇒ ∠A1+∠D1 = ∠E2
⇒ ∠D1 < ∠E2(ĐPCM)
b) Theo câu a) ta có: ∠A1+∠D1 = ∠E2
⇒ ∠A1 < ∠E2
⇒ BD< DC ( theo tính chất góc đối diện và cạnh tương ứng)
Vậy BD< DC
Trả lời 1:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
a)Trên AC lấy E sao cho AB = AE
Xét ΔABDΔABD và ΔAEDΔAED có
AB=AEA1ˆ=A2ˆADchungAB=AEA1^=A2^ADchung
⇒ΔABD=ΔAED(c.g.c)⇒ΔABD=ΔAED(c.g.c)
⇒D1ˆ=D2ˆ⇒D1^=D2^
Xét △AED có DECˆDEC^ là góc ngoài
⇒DECˆ>D2ˆ⇒DEC^>D2^ mà D2ˆ=D1ˆD2^=D1^
⇒DECˆ>D1ˆ⇒DEC^>D1^ (1)
Xét △ADC có D1ˆD1^ là góc ngoài tại đỉnh D
⇒D1ˆ>Cˆ⇒D1^>C^ (2)
Từ (1) và (2) ⇒DECˆ>Cˆ⇒DEC^>C^
Xét △DEC có: DECˆ>CˆDEC^>C^
⇒DC>ED⇒DC>ED (*)
Mà DE = DB (vì △ABD = △AED) (**)
Từ (*) và (**) ⇒DB<DC⇒DB<DC
Vậy…
b)
Xét △ABC có: AB < AC
⇒Cˆ<Bˆ⇒C^<B^ (quan hệ giữa cạnh và góc đối diện trong tam giác)
Xét △ADC có ADBˆADB^ là góc ngoài tại đỉnh D
⇒ADCˆ=A2ˆ+Cˆ⇒ADC^=A2^+C^
Xét ΔADBΔADB có ADCˆADC^ là góc ngoài tại đỉnh D
⇒ADBˆ=A1ˆ+Bˆ⇒ADB^=A1^+B^
Mà A1ˆ=A2ˆA1^=A2^ (AD là phân giác góc A); Cˆ<BˆC^<B^
⇒ADCˆ<ADBˆ