Câu hỏi:
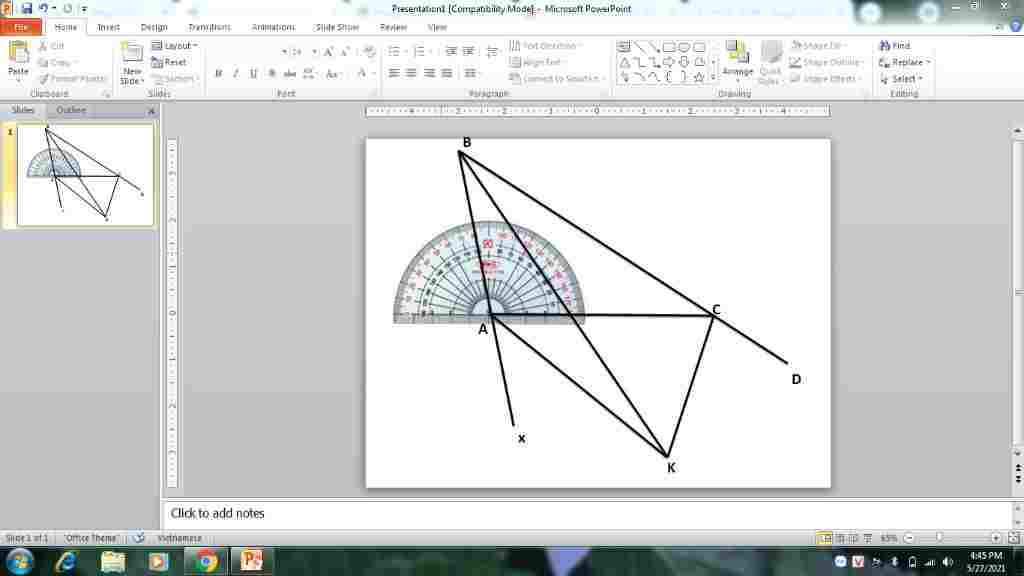
Giúp em bài tập về nhà Toán lớp 7 câu hỏi như sau: Cho tam giác abc có góc A=100 độ. Gọi CD là tia đối của tia CB. Tia phân giác của góc B cắt tia phân giác của góc ACD tại K. Tính góc BAK.
Mn ơi giúp mình với nha, mk cần ngay ạ.
Trả lời 2:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
Kẻ Ax đối AB
Kẻ KH ⊥ Ax
KL ⊥ CD
KM ⊥ AC
Ta có :
+ CK là phân giác ∠ ACD
Mà KL ⊥ CD
KM ⊥ AC
=> KL = KM ( Tính chất )
+ BK là phân giác ∠ ABC
Mà KH ⊥ Ax
KL ⊥ CD
=> KH = KL ( Tính chất )
Từ 2 điều trên => KM = KH
Ta có :
K nằm trong ∠ CAx
Mà KM ⊥ AC
KH ⊥ Ax
KM = KH
=> AK là phân giác ∠ CAx => ∠ CAK = 1/2 ∠ CAx
Mà ∠ CAx = 80° ( Kề bù với ∠ CAB )
=> ∠ CAK = 1/2 ∠ CAx = 1/2 . 80° = 40°
Ta có : ∠ CAB + ∠ CAK = ∠ BAK
100° + 40° = ∠ BAK
=> ∠ BAK = 140°
Vậy ∠ BAK = 140°
Trả lời 1:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
Gọi Ax là tia đối của tia AB
ΔABC có :
BK là tia phân giác của \hat{ABC}
CK là tia phân giác của góc ngoài \hat{ACB} (tức \hat{ACD})
Vì BK và CK cắt nhau tại K
⇒AK là tia phân giác của góc ngoài \hat{BAC}
Áp dụng định lý mở rộng :
Tia phân giác của 2 góc ngoài và tia phân giác của góc còn lại đồng quy
⇒AK là tia phân giác của \hat{xAC}
Vì \hat{xAC} và \hat{BAC} bù nhau
\hat{BAC}=100^o⇒\hat{xAC}=80^o
⇒\hat{KAC}=40^o
⇒\hat{BAK}=\hat{BAC}+\hat{KAC}
=100^o +40^o
=140^o