Câu hỏi:
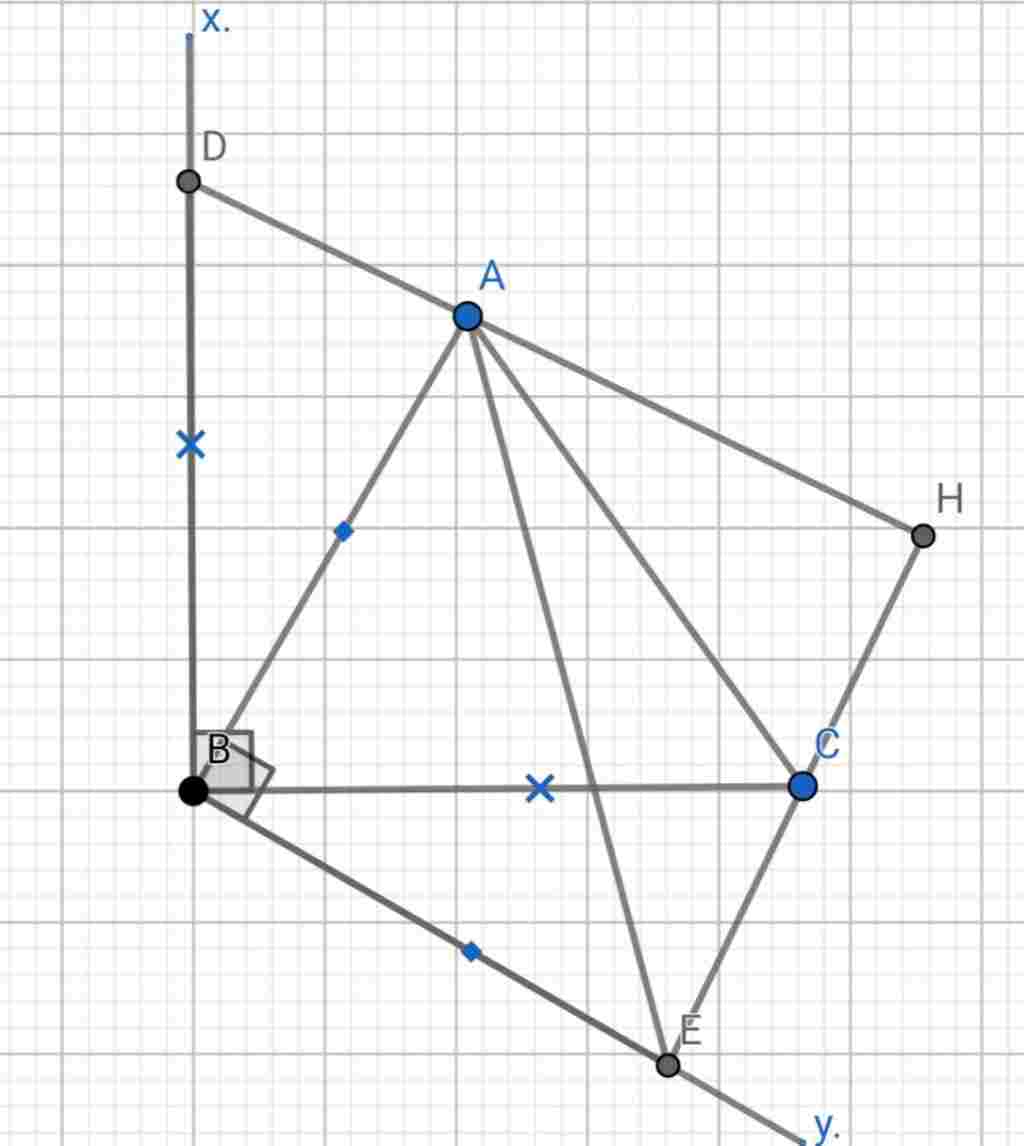
Giúp em bài tập về nhà Toán lớp 7 câu hỏi như sau: cho tam giác ABC có góc B <90 độ. TRên nửa mặt phẳng có chứa A bờ BC vẽ tia Bx vuông góc BC . TRên tia đó lấy D sao cho BD=BC. trên nửa mặt phẳng có chứa C bờ AB. vẽ tia By . góc BA, trên tia đó lấy E sao cho BE=BA.Chứng minh :
a) DA=CE,
b) DAvuoong góc CE,
gap lam a
Trả lời 2:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
Giải đáp: câu b
gọi H là giao điểm AD và CE
∧BAD+ ∧BAH= 180( kề bù)
mà ∧BAD= ∧BEC (vì ΔBAD=ΔBCE)
⇒∧BAH+ ∧BEC= 180
xét tứ giác ABEH có: (∧A+∧E)+∧B+∧H= 360 (tổng 4 góc trong tứ giác bằng 360)
⇒180+90+∧H=360
⇒∧H = 90 ⇒ DA⊥CE tại H
Lời giải và giải thích chi tiết:
Trả lời 1:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
a) $Bx\perp BC;D\in Bx$ (gt)
=>\hat{CBD}=90°
=>\hat{ABD}+\hat{ABC}=90°
$By\perp AB; E\in By$ (gt)
=>\hat{ABE}=90°
=>\hat{EBC}+\hat{ABC}=90°
$\\$
=>\hat{ABD}=\hat{EBC}
Xét $∆ABD$ và $∆EBC$ có:
AB=EB (gt)
\hat{ABD}=\hat{EBC} (c/m trên)
BD=BC (gt)
=>∆ABD=∆EBC (c-g-c)
=>DA=CE (hai cạnh tương ứng) (đpcm)
$\\$
b) Gọi $H$ là giao điểm của $DA$ và $EC$
Áp dụng tính chất tổng ba góc trong tam giác $180°$
Xét $∆ABE$ có:
\hat{BEA}+\hat{BAE}+\hat{ABE}=180°
Xét $∆AHE$ có:
\hat{HEA}+\hat{EAH}+\hat{AHE}=180°
=>(\hat{BEA}+\hat{HEA})+(\hat{BAE}+\hat{EAH})+\hat{ABE}+\hat{AHE}=180°+180°=360°
=>\hat{BEH}+\hat{BAH}+90°+\hat{AHE}=360° $\qquad (1)$
$\\$
Ta có \hat{BAD}=\hat{BEC} (do $∆ABD=∆EBC$ câu a)
Mà \hat{BAD}+\hat{BAH}=180° (hai góc kề bù)
=>\hat{BEC}+\hat{BAH}=180°
=>\hat{BEH}+\hat{BAH}=180° thay vào $(1)$ ta có:
180°+90°+\hat{AHE}=360°
=>\hat{AHE}=360°-(180°+90°)=90°
=>DA$\perp CE$ tại $H$ (đpcm)