Câu hỏi:
Giúp em bài tập về nhà Toán lớp 7 câu hỏi như sau: Cho góc nhọn xOy. Trên tia Ox lấy hai điểm A, C. Trên tia Oy lấy hai điểm B, D sao cho OA = OB , AC = BD
a, Chứng minh: AD=BC
b, Gọi E là giao điểm AD và BC. Chứng minh tam giác EAC = tam giác EBD
c, Chứng minh: OE là tia phân giác của góc xOy , OE vuông góc với CD.
Trả lời 2:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
thấy hay thì vote + đánh giá cho tớ nha
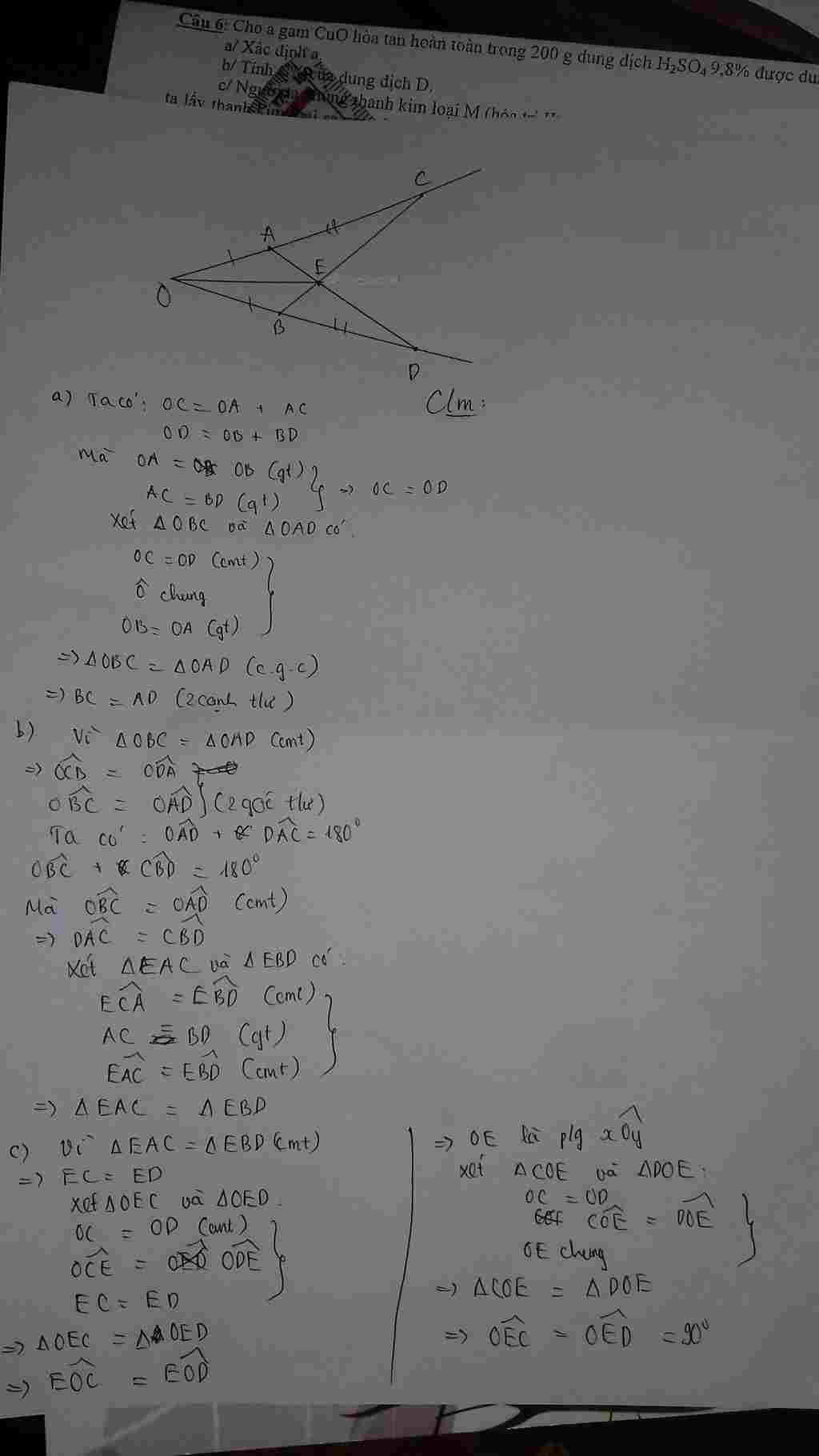
Trả lời 1:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
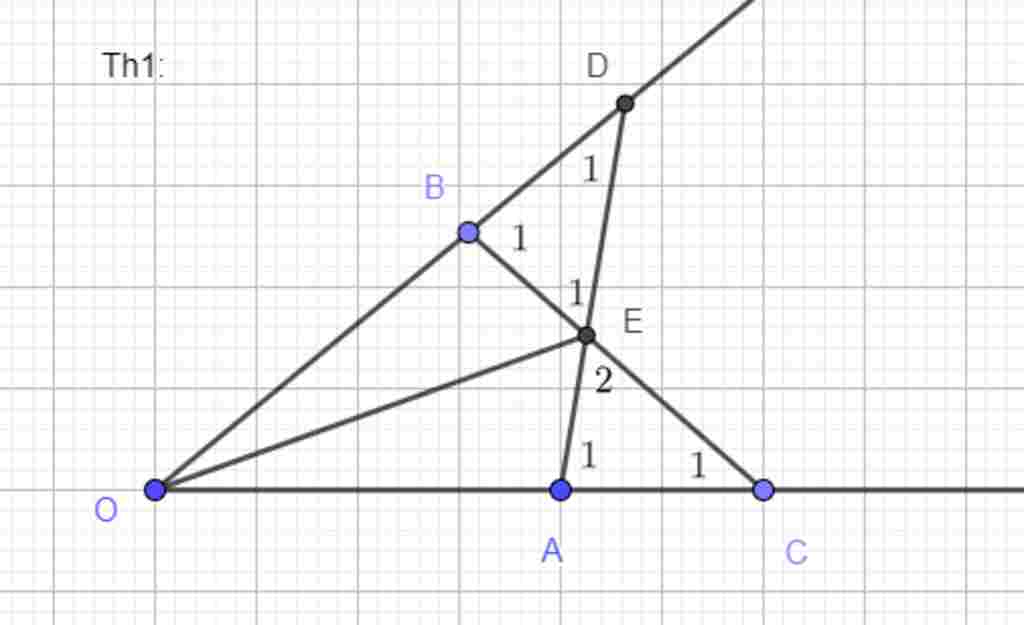
Th1:
a) Xét $\Delta OBC$ và $\Delta OAD$ có:
$OB=OA$ (gt)
$\widehat{O} $ chung
$OC=OA$ (gt)
$\Rightarrow \Delta OBC=\Delta OAD$ (c.g.c)
$\Rightarrow BC=AD$ (hai cạnh tương ứng)
b) Xét $\Delta EBD$ có:
$\widehat{E_1}+\widehat{B_1}+\widehat{D_1}=180^o\Rightarrow \widehat{B_1}=180^o-\widehat{E_1}-\widehat{D_1}$ (1)
Xét $\Delta EAC$ có:
$\widehat{E_2}+\widehat{A_1}+\widehat{C_1}=180^o\Rightarrow \widehat{A_1}=180^o-\widehat{E_2}-\widehat{C_1}$ (2)
mà $\widehat{E_1}=\widehat{E_2}$ (đối đỉnh) (3)
$\widehat{D_1}=\widehat{C_1}$ (do $\Delta OBC=\Delta OAD$ hai góc tương ứng) ($)
Từ 4 điều trên suy ra $\widehat{B_1}=\widehat{A_1}$
Ta có: $BD=OD-OB=OC-OA=AC$
Xét $\Delta EAC$ và $\Delta EBD$ có:
$\widehat{D_1}=\widehat{C_1}$
$BD=AC$ (cmt)
$\widehat{B_1}=\widehat{A_1}$
$\Rightarrow \Delta EAC=\Delta EBD$ (g.c.g)
c) $\Delta EAC=\Delta EBD\Rightarrow EC=ED$ (hai cạnh tương ứng)
$\Rightarrow $
Xét $\Delta OED$ và $\Delta OEC$ có:
$OD=OC$ (gt)
$\widehat{D_1}=\widehat{C_1}$
DE=CE (cmt)
$\Rightarrow \Delta OED=\Delta OEC$ (c.g.c)
$\Rightarrow \widehat{DOE}=\widehat{COE}$ (hai góc tương ứng)
$\Rightarrow OE$ là tiếp tuyến của $\widehat O$