Câu hỏi:
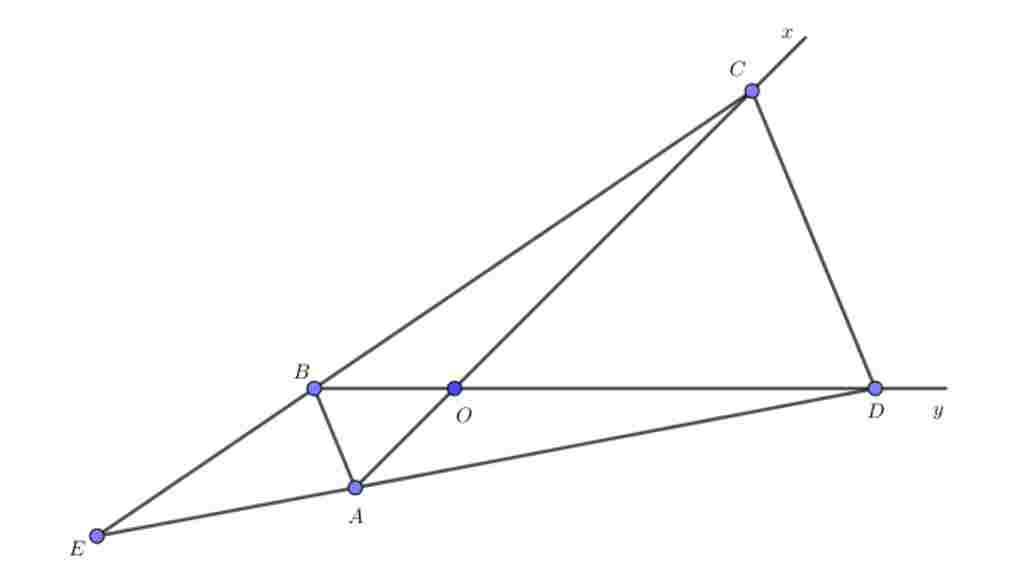
Giúp em bài tập về nhà Toán lớp 7 câu hỏi như sau: Cho góc nhọn xOy. Trên tia đối của tia Ox lấy điểm A, trên tia đối của tia Oy lấy điểm B sao cho OA = OB. Trên tia Ax lấy điểm C, trên tia By lấy điểm D sao cho AC = BD và OB<OD, OA<OC.
a) Chứng minh: AD = BC.
b) Gọi E là giao điểm của AD và BC. Chứng minh: EAC = EBD.
c) Chứng minh: AB//CD.
Trả lời 2:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
Giải đáp:
Lời giải và giải thích chi tiết:
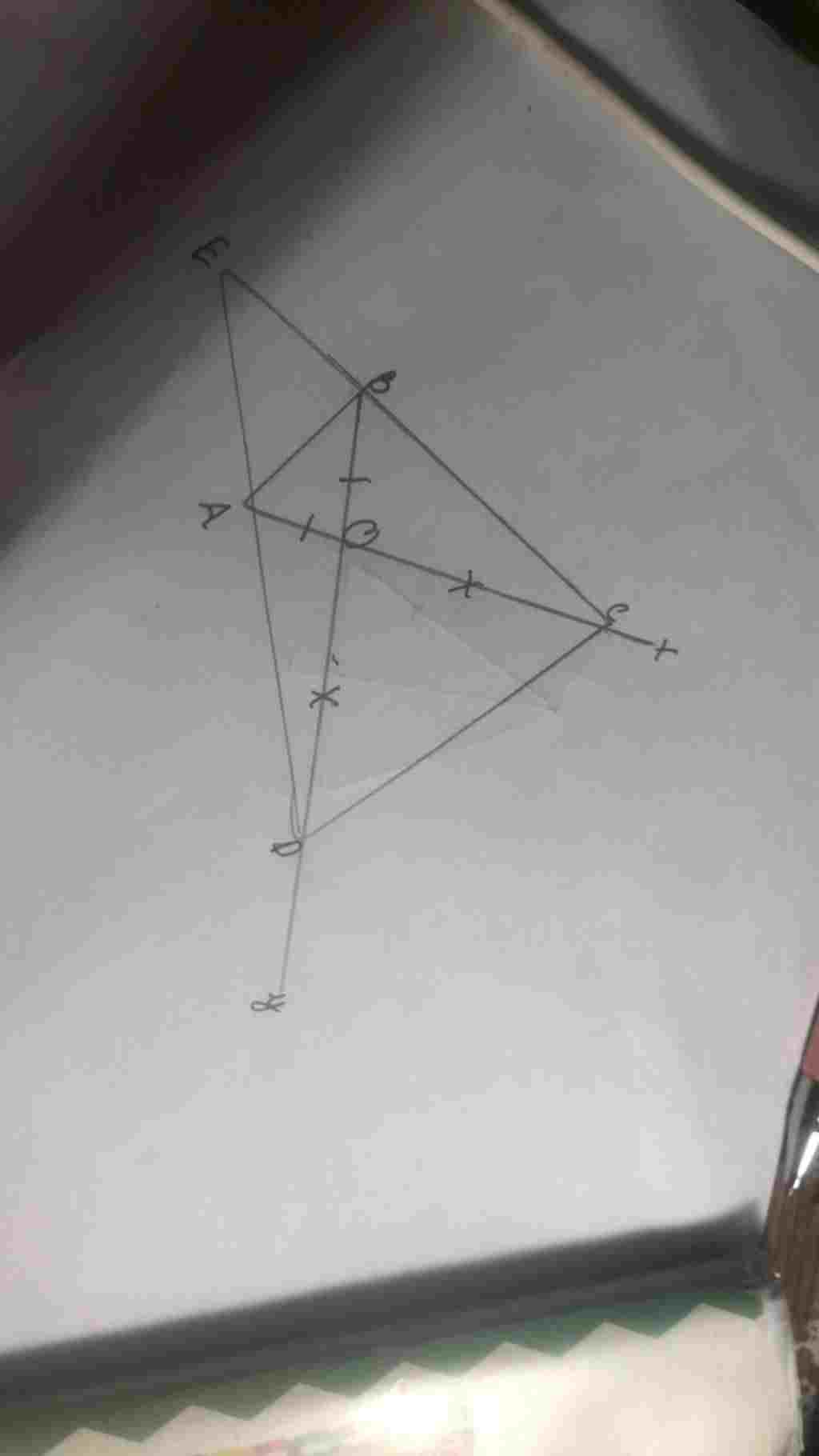
Vẽ hìn trong ảnh
a)Chứng minh:AD=BC
Xét Tam giác AOD và Tam giác BOC tao có:
OA=OB (gt) (1)
AC=BD(gt) (2)
Từ (1) và (2) => OC=OD (3)
Góc BOC =Góc AOD (đđ) (4)
Từ (1),(3) và (4) suy ra :
Tam giác AOD = Tam giác BOC ( c-g-c)
=> AD=BC ( 2 cạnh tương ứng) ( đpcm)
b) Gọi E là giao điểm của AD và BC.Chứng minh: Tam giác EAC = Tam giác EBD
Xét Tam giác EAC và Tam giác EBD:
BD=AC(gt) (5)
Tam giác AOD = Tam giác BOC (cmt) (6)
=> Góc ODA =Góc OCB (6)
Và Góc OAD = Góc OBC ( 7)
Mặt khác: Góc OAD + Góc CAE =180 độ ( kề bù) (8)
Góc OBC + Góc OBE = 180 độ ( kề bù) (9)
Từ (7),(8) và (9) => Góc CAE = Góc DBE(10)
Từ (5),(6) và (10) => Tam giác EAC =Tam giác EBD ( g-c-g) (đpcm)
c) Chứng minh: AB//CD
Xét Tam giác DAC và Tam giác CBD
CD là cạnh chung
BD=AC (gt)
AD=BC (cmt)
Vậy tam giác DAC = tam giác CBD ( c-c-c)
=> Góc BDC =Góc ACD ( 2 góc tương ứng) (11)
Xét Tam giác ABD và tam giác BAC
BD=AC (gt)
Góc ADB= Góc BCA (cmt)
AD=BC (cmt)
Vậy Tam giác ABD = tam giác BAC (c-g-c)
=> Góc ABD = Góc BAC ( 2 góc tương ứng) (12)
Mặt khác:
Góc AOB = Góc DOC (đđ) (13)
Từ (11),(12)và (13) suy ra:
GÓc ABD = Góc BDC
=> AB//CD ( cặp góc so le trong bằng nhau) (đpcm)
Xin vote 5sao và ctlhn
~ Học tốt nhen~
Trả lời 1:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
Giải đáp:
a)
Ta có:
$AC=OA+OC$
$BD=OB+OD$
mà $AC=BD$ (gt) , $OA=OB$ (gt)
$\Rightarrow OC=OD$
Xét $\triangle OAD$ và $\triangle OBC$ có
$OA=OB$ (gt)
$\widehat{AOD}=\widehat{BOC}$ (đối đỉnh)
$OD=OC$ (cmt)
$\Rightarrow \triangle OAD=\triangle OBC$ (c.g.c)
$\Rightarrow AD=BC$ (hai cạnh tương ứng)
b)
Do $\triangle OAD=\triangle OBC$ (cmt)
$\Rightarrow \widehat{ODA}=\widehat{OCB}$ (hai góc tương ứng)
và $\widehat{OAD}=\widehat{OBC}$ (hai góc tương ứng)
Ta có:
$\widehat{OAD}+\widehat{CAE}=180^0$
$\widehat{OBC}+\widehat{DBE}=180^0$
mà $\widehat{OAD}=\widehat{OBC}$ (cmt)
$\Rightarrow \widehat{CAE}=\widehat{DBE}$
Xét $\triangle EAC$ và $\triangle EBD$ có
$\widehat{CAE}=\widehat{DBE}$ (cmt)
$AC=BD$ (gt)
$\widehat{ACE}=\widehat{EDB}$ (do $\widehat{OCB}=\widehat{ODA}$ -cmt)
$\Rightarrow \triangle EAC=\triangle EBD$ (g.c.g)
c)
Xét $\triangle AOB$ có $OA=OB$ (gt)
$\Rightarrow \triangle AOB$ cân tại $O$
$\Rightarrow \widehat{OBA}=\widehat{OAB}$
Xét $\triangle COD$ có $OC=OD$ (cmt)
$\Rightarrow \triangle COD$ cân tại $O$
$\Rightarrow \widehat{OCD}=\widehat{ODC}$
Ta có:
$\widehat{AOB}+\widehat{OBA}+\widehat{OAB}=180^0$
$\widehat{COD}+ \widehat{OCD}+\widehat{ODC}=180^0$
mà $ \widehat{OBA}=\widehat{OAB}$(cmt), $ \widehat{OCD}=\widehat{ODC}$ (cmt)
$\Rightarrow \widehat{AOB}+2\widehat{OBA}=180^0$
$\widehat{COD}+ 2\widehat{ODC}=180^0$
mà $\widehat{AOB}=\widehat{COD}$ (đối đỉnh)
$\Rightarrow \widehat{OBA}=\widehat{ODC}$
mà chúng ở vị trí so le trong
$\Rightarrow AB//CD$