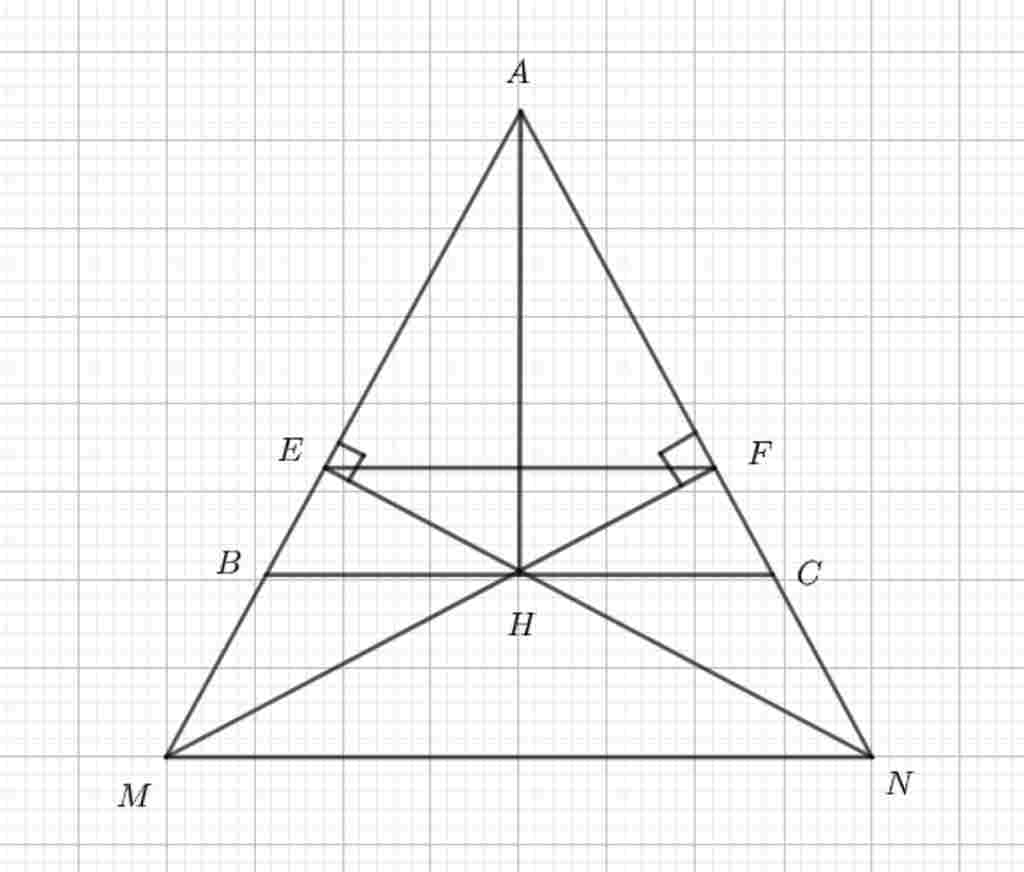
Câu hỏi:
Giúp em bài tập về nhà Toán lớp 7 câu hỏi như sau: Cho tam giác ABC nhọn có AB=AC, H là trung điểm của BC.Từ H kẻ HE vuông góc với AB tại E, HF vuông góc với AC tại F
a) Chứng minh rằng: tam giác ABH bằng tam giác ACH
b) Chứng minh rằng:tam giác AHE bằng tam giác AHF
c) Gọi M là giao điểm của đường thẳng AB và đường thẳng HF, N là giao điểm của đường thẳng AC và đường thẳng HE.Chứng minh rằng:ME=NF ; MF=NE
d) Chứng minh rằng: EF song song MN
Trả lời 1:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
a) Xét $\Delta ABH$ và $\Delta ACH$ óc:
$AB=AC$ (giải thiết)
$AH$ chung
$BH=CH$ (do giải thiết cho $H$ là trung điểm của $BC$)
$\Rightarrow \Delta ABH=\Delta ACH$ (c.c.c)
b) Theo chứng minh ở câu a $\Delta ABH=\Delta ACH$
$\Rightarrow \widehat{BAH}=\widehat{CAH}$ (2 góc tương ứng)
Hay $\widehat{EAH}=\widehat{FAH}$
Xét $\Delta$ vuông $AHE$ và $\Delta$ vuông $AHF$ có:
$\widehat{EAH}=\widehat{FAH}$
$AH$ chung
$\Rightarrow \Delta$ vuông $AHE=\Delta$ vuông $AHF$ (cạnh huyền-góc nhọn)
c) Do $\Delta$ vuông $AHE=\Delta$ vuông $AHF\Rightarrow HE=HF$ (2 cạnh tương ứng)
Xét $\Delta $ vuông $HEM$ và $\Delta$ vuông $HFN$ có:
$HE=HF$
$\widehat{EHM}=\widehat{FHN}$ (đối đỉnh)
$\Rightarrow \Delta $ vuông $HEM=\Delta$ vuông $HFN$ (cạnh góc vuông-góc nhọn)
$\Rightarrow ME=NF$ (2 cạnh tương ứng)
Và $MH=NH$ (2 cạnh tương ứng) và có $HE=HF$ (chứng minh ở trên)
$MF=MH+HF=NH+HE=NE$ (điều phải chứng minh)
d) Ta có $ME=NF$ và $AE=AF$
Nên $AM=AE+ME=AF+NF=AN$
$AM=AN\Rightarrow \Delta AMN$ cân đỉnh $A$
nên $\widehat{AMN}=\widehat{ANM}$
Theo tính chất tổng 3 góc trong 1 tam giác $\widehat{AMN}+\widehat{ANM}+\widehat{A}=180^o$
$\Rightarrow 2\widehat{AMN}+\widehat A=180^o$
$\Rightarrow \widehat{AMN}=\dfrac{180^o-\widehat A}{2}$ (1)
Tương tự ta có $AE=AF\Rightarrow \Delta AEF$ cân đỉnh $A$
$\Rightarrow \widehat{AEF}=\widehat{AFE}=\dfrac{180^o-\widehat A}{2}$ (2)
Từ (1) và (2) suy ra $\widehat{AMN}=\widehat{AEF}$ mà chúng ở vị trí đồng vị nên
$MN\parallel EF$ (đpcm).