Câu hỏi:
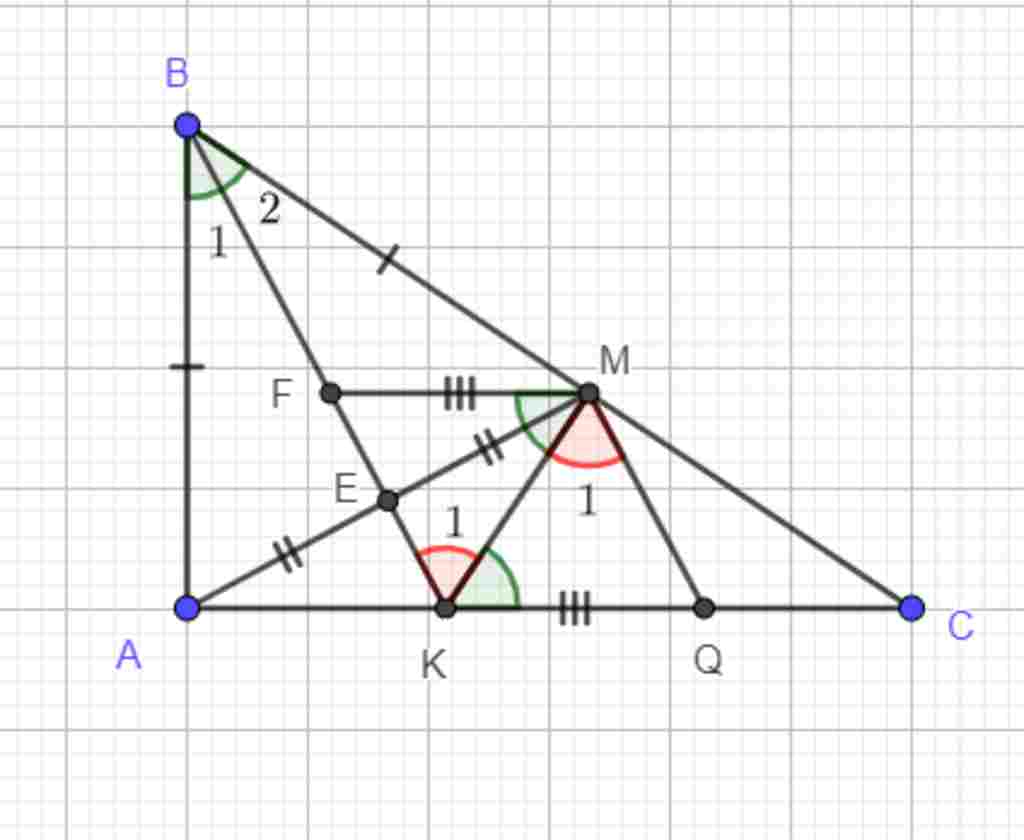
Giúp em bài tập về nhà Toán lớp 7 câu hỏi như sau: Bài tập: Cho tam giác ABC vuông tại A (AB<AC). Trên cạnh BC lấy điểm M sao cho BA=BM. Gọi E là trung điểm của AM.
a. Chứng minh tam giác ABE = tam giác MBE
b. Gọi K là giao điểm của BE và AC. Chứng minh KM vuông góc BC
c. Qua M vẽ đường thẳng // với AC, cắt BK tại F. Trên đoạn thẳng KC lấy Q sao cho KQ=MF. chứng minh góc ABK = góc QMC.
Trả lời 2:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
Giải đáp:
Lời giải và giải thích chi tiết:
a) Tg AEB = MEB (c-c-c)
b) Có tg ABM cân tại B mà BE là trung tuyến ==> BE là p/g
==> góc ABK = MBK
=> Tg ABK = MBK (c-g-c)
==> Góc A = góc KMB = 90 độ
c) Có MF // AC ==> MF // KQ ==> MFKQ là hbh
==> MQ // KF ==> MQ // BK
==> Góc QMC = KBC
Mà góc KBC = ABK ( Vì BE là p/g )
==> Góc QMC = ABK
Trả lời 1:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
a) Xét $\Delta ABE$ và $\Delta MBE$ có:
$BA=BM$ (giả thiết)
$BE$ chung
$AE=ME$ (giả thiết)
$\Rightarrow \Delta ABE=\Delta MBE$ (c.c.c)
b) Xét $\Delta ABK$ và $MBK$ có:
$AB=MB$ (giả thiết)
$\widehat{B_1}=\widehat{B_2}$ (*) (hai góc tương ứng do $\Delta ABE=\Delta MBE$ câu a)
$BK$ chung
$\Rightarrow \Delta ABK=MBK$ (c.g.c)
$\Rightarrow\widehat{BAK}=\widehat{BMK}=90^o$ (hai góc tương ứng)
$\Rightarrow BC\bot KM$ (đpcm)
c) Xét $\Delta FMK$ và $\Delta QKM$ có:
$FM=QK$ (giả thiết)
$\widehat{FMK}=\widehat{QKM}$ (hai góc ở vị trí so le trong do $FM\parallel KQ$)
$KM$ chung
$\Rightarrow \Delta FMK=\Delta QKM$ (c.g.c)
$\Rightarrow \widehat{FKM}=\widehat{QMK}$ (hai góc tương ứng)
Hay $\widehat{K_1}=\widehat{M_1}$ mà chúng ở vị trí so le trong nên suy ra $MQ\parallel BK$
$\Rightarrow \widehat{B_2}=\widehat{QMC}$ (**) (2 góc ở vị trí đồng vị)
Từ (*) và (**) suy ra $\widehat{B_1}=\widehat{QMC}$ (đpcm)