Câu hỏi:
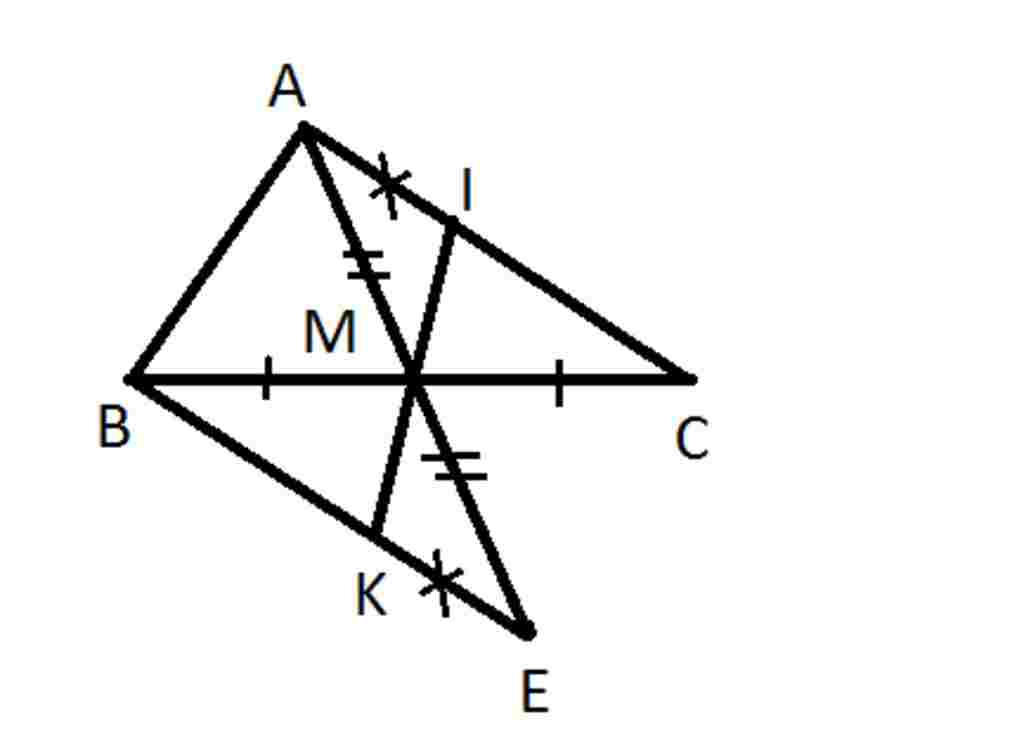
Giúp em bài tập về nhà Toán lớp 7 câu hỏi như sau: Cho tam giác ABC ,M là trung điểm của BC.Trên tia đối của tia MA lấy điểm E sao cho ME=MA
a,CM tam giác AMC= tam giác EMB
b,AC// BE
C, Gọi I là 1 điểm trên AC ,K là 1 điểm trên EB sao cho AI=EK
CM 3 điểm I,M,K thẳng hàng
Trả lời 2:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
Giải đáp:
Lời giải và giải thích chi tiết:
a/ Xét tam giác AMB và tam giác EMC có:
BM = MC (M là trung điểm của BC)
góc AMB = góc EMC (đđ)
AM = EM (GT)
=> tam giác AMB = tam giác EMC.
b/ Xét tam giác AMC và tam giác EMB có:
AM = EM (GT)
góc AMC = góc EMB (đđ)
BM = MC (M là trung điểm BC)
=> tam giác AMC = tam giác EMB.
=> góc CAM = góc MEB (hai góc t/ư)
Mà hai góc này ở vị trí slt
=> AC // BE.
c/ Ta có: AB = CE (tam giác AMB = tam giác EMC)
Mà BI = CK (GT)
=> AB – BI = EC – CK
hay AI = EK.
Xét tam giác AMI và tam giác EMK có:
AM = EM (GT)
góc IAM = góc KEM (tam giác AMB = tam giác EMC)
AI = EK (cmt)
=> tam giác AMI = tam giác EMK.
=> góc AMI = góc EMK (hai góc t/ư)
Mà ta có: góc EMK + góc AMK = 1800 (kề bù)
=> góc AMI + góc AMK = 1800
hay góc IMK = 1800.
hay I; M; K thẳng hàng.
—> đpcm.
Trả lời 1:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
$\text{a) Xét ΔAMC và ΔEMB có:}$
$\text{AM = EM (giả thiết)}$
$\widehat{AMC}$ = $\widehat{EMB}$ $\text{(đối đỉnh)}$
$\text{MC = MB (M trung điểm BC)}$
⇒ $\text{ΔAMC = ΔEMB (c.g.c) (1)}$
$\text{b) Từ (1) ⇒ $\widehat{MBE}$ = $\widehat{MCA}$ (2 góc tương ứng)}$
$\text{mà 2 góc này ở vị trí so le trong}$
⇒ $\text{AC // BE }$
$\text{c) Xét ΔAMI và ΔEMK có:}$
$\text{AM = EM (giả thiết)}$
$\text{Từ (1)}$ ⇒ $\widehat{IAM}$ = $\widehat{KEM}$ $\text{(2 góc tương ứng)}$
$\text{AI = EK (giả thiết)}$
⇒ $\text{ΔAMI = ΔEMK (c.g.c)}$
⇒ $\widehat{AMI}=\widehat{EMK}$ (hai góc tương ứng bằng nhau) (1)
Mà $\widehat{AMI}+\widehat{IME}=180^o$ (do $A, M, E\text{thẳng hàng nên }\widehat{AME}$ là góc bẹt) (2)
thay (1) vào (2)
$\Rightarrow\widehat{EMK}+\widehat{IME}=180^o$
$\Rightarrow\widehat{IMK}=180^o$ là góc bẹt
$\Rightarrow I, M, K$ thẳng hàng.