Câu hỏi:
Giúp em bài tập về nhà Toán lớp 12 câu hỏi như sau: có bao nhiêu số phức z thoả |z-2-i|=|z-3i| và |z-2-3i|<=2
Trả lời 2:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
Giải đáp:
Vô số
Lời giải và giải thích chi tiết:
$\bullet$|z-2-i|=|z-3i| (z=a+bi)
<=>|a+bi-2-i|=|a+bi-3i|
<=>\sqrt{(a-2)^2+(b-1)^2}=\sqrt{a^2+(b-3)^2}
<=>(a-2)^2+(b-1)^2=a^2+(b-3)^2
<=>a^2-4a+4+b^2-2b+1=a^2+b^2-6b+9
<=>-4a+4b=4
<=>-a+b=1
<=>b=a+1
=>z=a+(a+1)
$\bullet$ |z-3-3i|<=2
<=>|a+(a+1)i-2-3i|<=2
<=>\sqrt{(a-2)^2+(a+1-3)^2}<=2
<=>\sqrt{2(a-2)^2}<=2
<=>|a-2|<=\sqrt{2}
TH 1:
@a-2>=0
<=>a>=2
@a-2<=\sqrt{2}
<=>a<=2+\sqrt{2}
=>2<=a<=2+\sqrt{2}
TH 2:
@a-2<0
<=>a<2
@2-a<=\sqrt{2}
<=>2-\sqrt{2}<=a
=>2\sqrt{2}<=a<2
Vậy, có vô số số thức z
Trả lời 1:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
Giải đáp:
Vô số
Lời giải và giải thích chi tiết:
Gọi $z= x + yi\quad (x;y\in\Bbb R)$
và $M$ là điểm biểu diễn số phức $z$ trên mặt phẳng phức
$\bullet\quad |z-2-i| = |z-3i|$
$\Leftrightarrow |(x-2) + (y-1)i| = |x + (y-3)i|$
$\Leftrightarrow \sqrt{(x-2)^2 + (y-1)^2} = \sqrt{x^2 + (y-3)^2}$
$\Leftrightarrow (x-2)^2 + (y-1)^2 = x^2 + (y-3)^2$
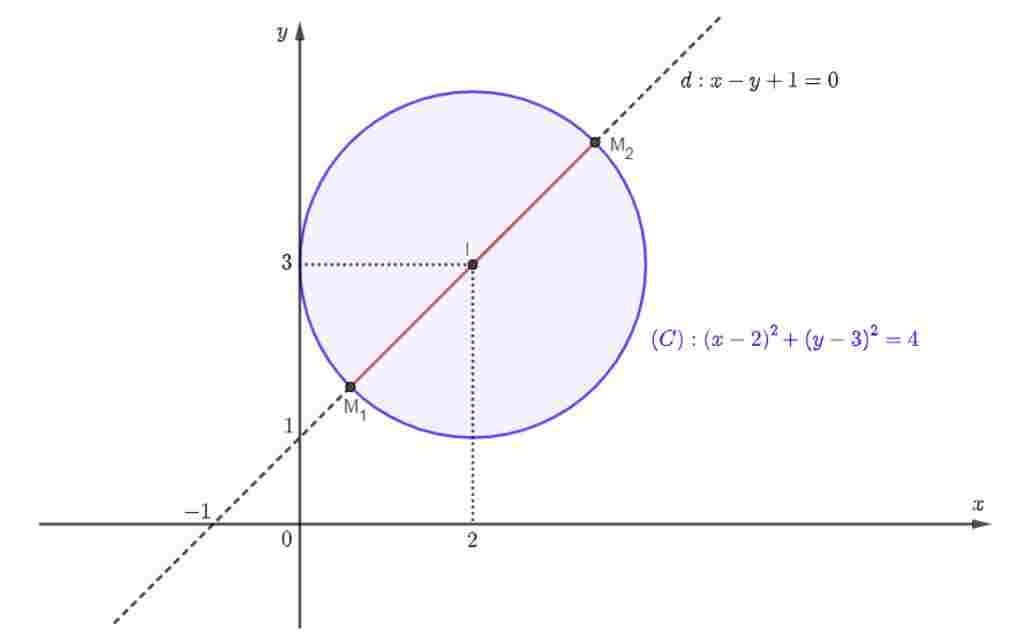
$\Leftrightarrow x -y + 1 =0$
$\Rightarrow$ Tập hợp các điểm $M$ là đường thẳng $d: x-y+1 =0$
$\bullet\quad |z-2-3i| \leqslant 2$
$\Leftrightarrow |(x-2) + (y-3)i| \leqslant 2$
$\Leftrightarrow \sqrt{(x-2)^2 + (y-3)^2} \leqslant 2$
$\Leftrightarrow (x-2)^2 + (y-3)^2 \leqslant 4$
$\Rightarrow$ Tập hợp các điểm $M$ là hình tròn $(C)$ tâm $I(2;3),$ bán kính $R = 2$ (tính cả biên)
Ta có:
$I(2;3)\in d \Rightarrow d$ cắt $(C)$ tại hai điểm $M_1;M_2$
Do đó, tập hợp các điểm $M$ là đoạn thẳng $M_1M_2$
Với mỗi điểm $M\in M_1M_2$ ta được một số phức $z$ tương ứng
Vậy có vô số số phức $z$ thỏa mãn đề bài