Câu hỏi:
Giúp em bài tập về nhà Toán lớp 12 câu hỏi như sau: 1 Cho số phức z = 2 – 2i. Tìm khẳng định sai.
A. Phần thực của z là: 2.
B. Phần ảo của z là: -2.
C. Số phức liên hợp của z là z− = -2 + 2i.
D. Môđun của z là
Câu 2: Cho số phức z = -1 + 3i. Phần thực, phần ảo của z− là
A. -1 và 3 B. -1 và -3 C. 1 và -3 D. -1 và -3i.
Câu 3: Môđun của số phức z thỏa mãn z− = 8 – 6i là
A. 2 B. 10 C. 14 D. 2√7
Câu 4: Tìm các số thực x, y sao cho (x – 2y) + (x + y + 4).i = (2x + y) + 2yi.
A. x = 3, y = 1 B. x = 3, y = -1
C. x = -3, y = -1 D. x = -3, y = 1
Câu 5: Hai số phức z1 = x – 2i, z22 + yi (x, y ∈ R) là liên hợp của nhau khi
A. x = 2, y = -2 B. x = -2, y = -2 C. x = 2, y = 2 D. x = -2, y = 2
Câu 6: Tập hợp các điểm biểu diễn số phức z thòa mãn |z| = |1 + i| là
A. Hai điểm B. Hai đường thẳng
C. Đường tròn bán kính R=2 D. Đường tròn bán kính R= √2 .
Trả lời 2:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
Giải đáp:
Lời giải và giải thích chi tiết:
câu 1 là câu c vì liên hợp của số z là 2+2i
câu 2 ta có liên hợp của z là -1 -3i nên phần thực là -1 và phần ảo là -3
câu 3 có liên hợp của số phức z là 8 -6i ⇒ z là 8+6i ⇒ môđun của z là $\sqrt[2]{8^{2} + (-6)^{2} }$
câu 5 z1=x-2i và z2=2+yi liên hợp vs nhau khi x=2 và y=2
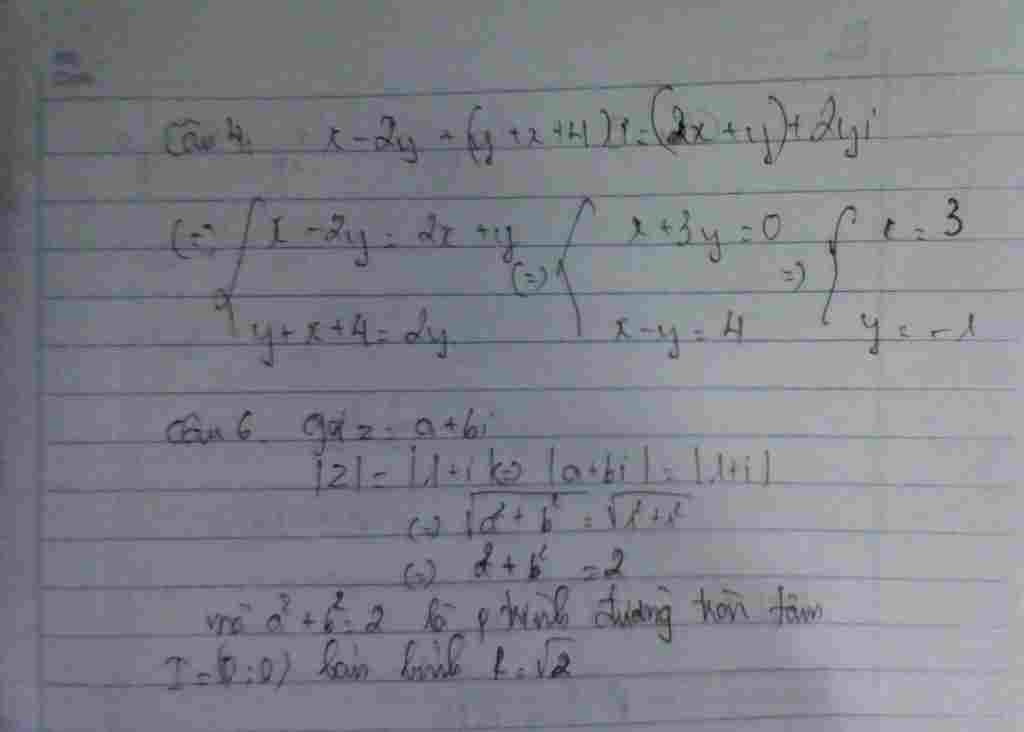
Trả lời 1:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
Giải đáp:
1) C
2) B
3) B
4) D
5) C
6) D
Lời giải và giải thích chi tiết:
1) Số phức $z = 2 – 2i$ có:
– Phần thực là: $a = 2$
– Phần ảo là: $b = -2$
– Môđun là: $|z|=\sqrt{2^2 + (-2)^2}= 2\sqrt2$
– Số phức liên hợp là: $\overline{z}= 2 + 2i$
2) Số phức $z = – 1 + 3i$
Số phức liên hợp của $z$ là $\overline{z}= -1 – 3i$
Khi đó, $\overline{z}$ có:
– Phần thực là: $a = -1$
– Phần ảo là: $b = -3$
3) $\overline{z}= 8 – 6i$
Ta có:
$|z|=|\overline{z}|=\sqrt{8^2 + (-6)^2}= 10$
4) $(x-2y) + (x+y+4)i = (2x+y) + 2yi$
$\Leftrightarrow \begin{cases}x- 2y = 2x + y\\x+ y + 4 = 2y\end{cases}$
$\Leftrightarrow \begin{cases}x+ 3y = 0\\x – y = -4\end{cases}$
$\Leftrightarrow \begin{cases}x = -3\\y = 1\end{cases}$
5) $z_1 = x – 2i$
$z_2 = 2 + yi$
$z_1$ và $z_2$ là hai số phức liên hợp
$\Leftrightarrow \begin{cases}x = 2\\-2= -y\end{cases}$
$\Leftrightarrow \begin{cases}x = 2\\y = 2\end{cases}$
6) Gọi $z = a + bi\ (a,\ b\in\Bbb R)$
Ta có:
$\quad |z| = |1 + i|$
$\Leftrightarrow \sqrt{a^2 + b^2}= \sqrt{1^2 + 1^2}$
$\Leftrightarrow a^2 + b^2 = 2$
Tập hợp số phức $z$ thoả mãn đề bài là một đường tròn tâm $O(0;0)$ bán kính $R = \sqrt2$





