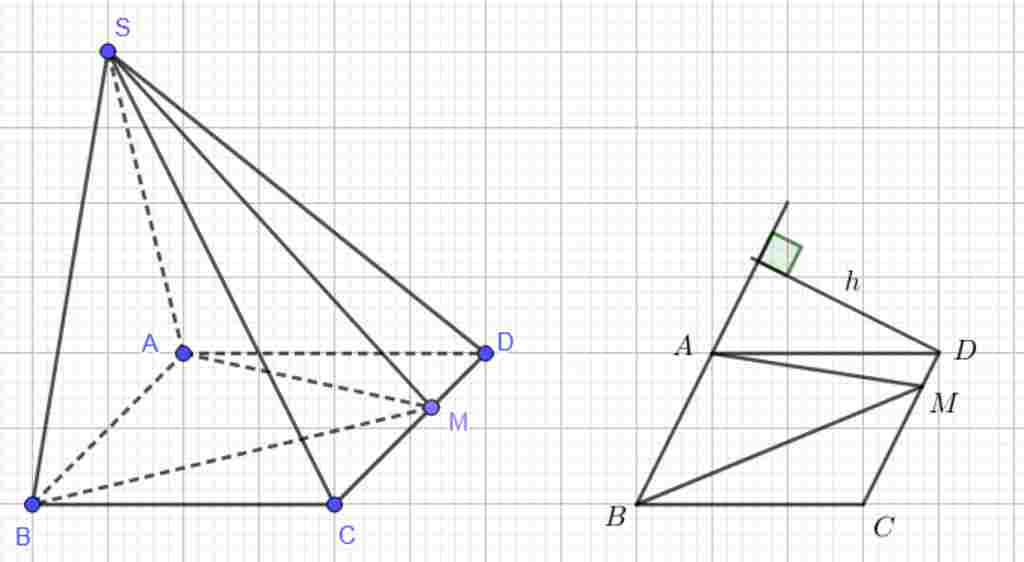
Câu hỏi:
Giúp em bài tập về nhà Toán lớp 12 câu hỏi như sau: Khối chóp S.ABCD có thể tích bằng V. Lấy điểm M trên cạnh CD, tính theo V thể tích khối chóp S.ABM biết ABCD là hình bình hành.
A. V/2 B. 2V/3 C. V/3 D. V/6
Trả lời 2:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
Giải đáp:A
Lời giải và giải thích chi tiết:
Vì diện tích của ΔABM =1/2 diện tích của hbh ABCD
Mà đường cao của 2 hình chóp là như nhau
⇒ V S.ABM=1/2 V S.ABCD
=1/2V
Trả lời 1:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
Giải đáp: A: $V_{SABM}=\dfrac{V}{2}$
Lời giải và giải thích chi tiết:
Ta có: $V=V_{SABCD}=\dfrac{1}{3}d_{(S,(ABC))}.S_{ABCD}$
$V_{SABM}=\dfrac{1}{3}d_{(S,(ABM))}.S_{ABM}$
$\Rightarrow \dfrac{V}{V_{SABM}}=\dfrac{S_{ABCD}}{S_{ABM}}$
Mà $S_{ABCD}=h.AB$ $(h=d_{(D,AB)}=d_{(M,AB)})$
$S_{ABM}=\dfrac{1}{2}h.AB$
$\Rightarrow \dfrac{V}{V_{SABM}}=\dfrac{1}{\dfrac{1}{2}}=2$
$\Rightarrow V_{SABM}=\dfrac{V}{2}$