Câu hỏi:
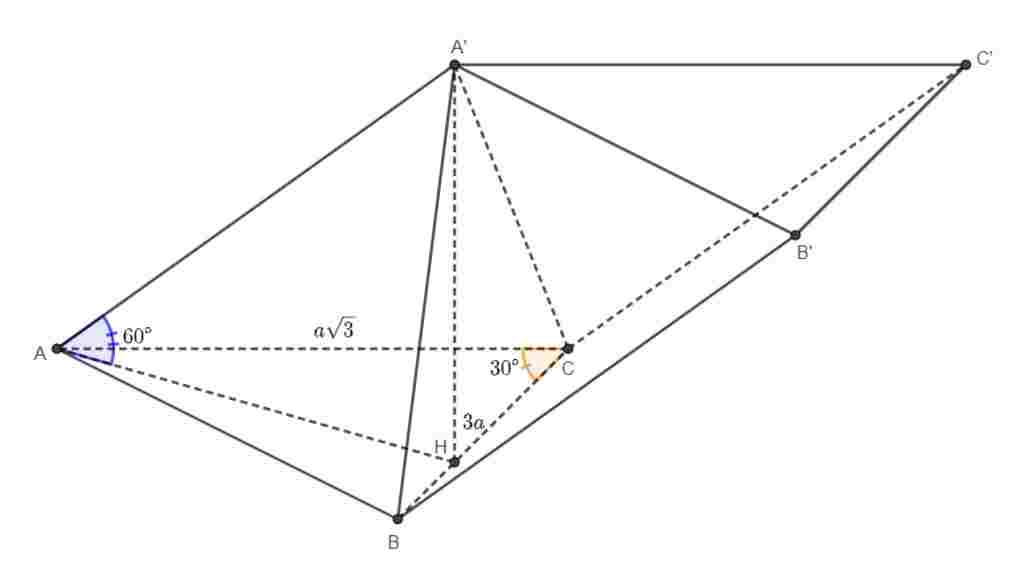
Giúp em bài tập về nhà Toán lớp 12 câu hỏi như sau: Cho lăng trụ ABC.A’B’C’ có AC=a√3, BC=3a, góc ACB=30 độ. Gọi H là điểm nằm trên cạnh BC sao cho HC=2HB. Hai mặt phẳng (A’AH) và (A’BC) cùng vuông góc với (ABC). Cạnh bên hợp với đáy một góc 60 độ. Thể tích khối lăng trụ ABC.A’B’C’ là
Trả lời 1:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
Giải đáp:
$V_{ABC.A’B’C’} = \dfrac{9a^3}{4}$
Lời giải và giải thích chi tiết:
Xét $ΔABC$ có:
$AC = a\sqrt3;\, BC = 3a;\, \widehat{ACB} = 30^\circ$
$\to S_{ABC} = \dfrac12AC.BC.\sin\widehat{ACB} = \dfrac12\cdot a\sqrt3\cdot 3a\cdot\sin30^\circ$
$\to S_{ABC} = \dfrac{3a^2\sqrt3}{4}$
Ta có:
$HC = 2HB$
$\to HC = \dfrac23BC = a$
Áp dụng định lý $\cos$ ta được:
$AH^2 = AC^2 + HC^2 – 2AC.HC.\cos\widehat{ACH}$
$\to AH^2 = 3a^2 + a^2 – 2a\sqrt3.a.\cos30^\circ$
$\to AH^2 = a^2$
$\to AH = a$
Mặt khác:
$\begin{cases}(A’AH)\perp (ABC)\\(A’BC)\perp (ABC)\\(A’AH)\cap (A’BC) = A’H\end{cases}$
$\to A’H\perp (ABC)$
$\to \widehat{(A’A;(ABC))} = \widehat{A’AH} = 60^\circ$
$\to A’H = AH.\tan60^\circ = a\sqrt3$
Ta được:
$V_{ABC.A’B’C’} = S_{ABC}.A’H = \dfrac{3a^2\sqrt3}{4}\cdot a\sqrt3 = \dfrac{9a^3}{4}$