Câu hỏi:
Giúp em bài tập về nhà Toán lớp 12 câu hỏi như sau: Cho hình hộp đứng có đáy là hình thoi cạnh
a và có góc nhọn bằng 60 độ . Đường chéo lớn của đáy bằng đường chéo nhỏ của lăng trụ. Tính thể tích hình hộp?
Trả lời 2:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
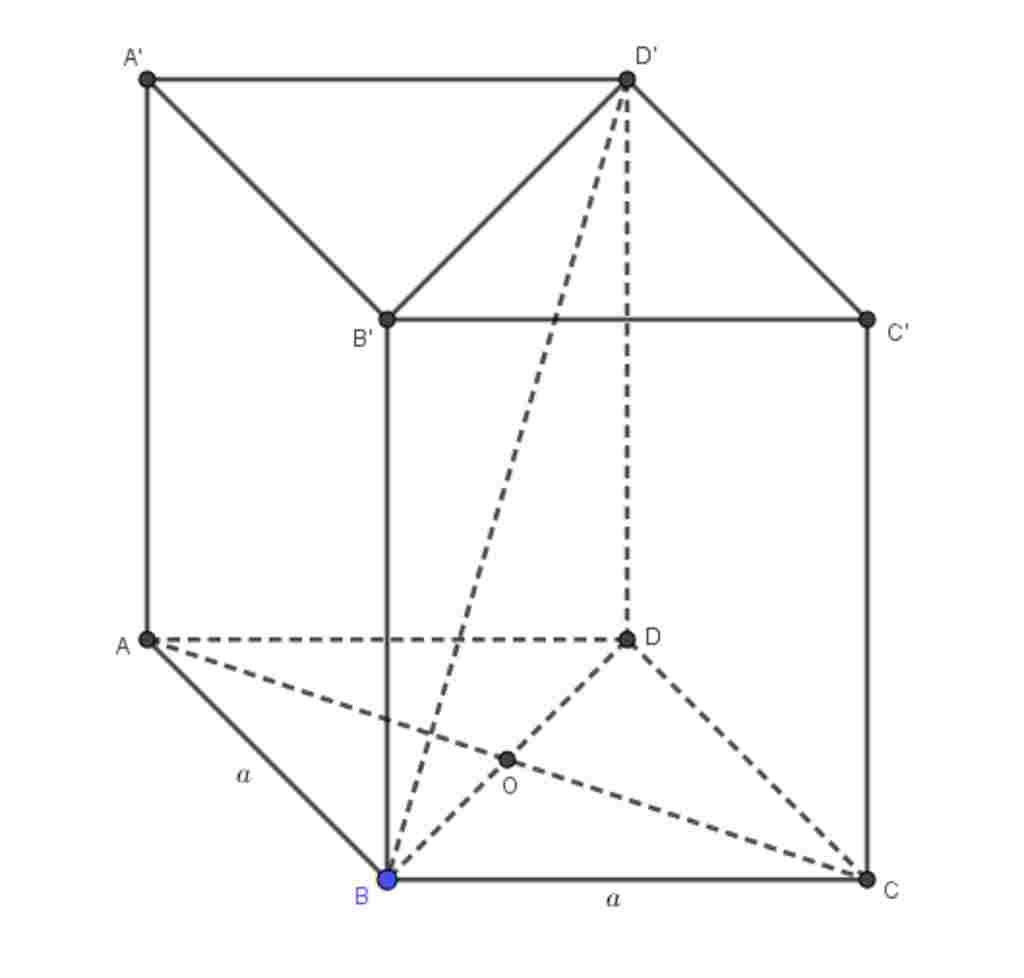
text{Gọi} AC cap BD = {O}
text{Ta có}
ABCD text{là hình thoi cạnh a}
hat{BAD} = 60^0
-> ΔABD text{đều}
-> AB = AD = BD = a
-> DO = OB = a/2
text{Xét ΔAOB vuông tại O có}
AB^2 = AO^2 + OB^2 (text{Định lí Pythagoras})
-> AO = sqrt{AB^2 – OB^2} = sqrt{a^2 – (a/2)^2} = (a\sqrt{3})/2
-> AC = 2AO = asqrt{3}
text{Theo giả thuyết}
-> AC = BD’ = asqrt{3}
text{Xét ΔBDD’ vuông tại D có}
BD’^2 = BD^2 + DD’^2 (text{Định lý Pythagoras})
-> DD’ = sqrt{BD’^2 – BD^2} = sqrt{(a\sqrt{3})^2 – a^2} = asqrt{2}
-> V = S_{ABCD}.DD’ = 1/(2).a.asqrt{3}.asqrt{2} = (a^{3}\sqrt{6})/2
Trả lời 1:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
Giải đáp:
$V= \dfrac{a^3\sqrt6}{2}$
Lời giải và giải thích chi tiết:
Xét lặng trụ đứng $ABCD.A’B’C’D’$ có đáy là hình thoi cạnh $a$, $\widehat{BAD} =60^\circ$
$\to ΔBAD;\, ΔBCD$ đều
Gọi $AC\cap BD=\{O\}$
$\to \begin{cases}AC = 2AO = AB\sqrt3 = a\sqrt3\\BD = AB = AD = BC = CD = a\end{cases}$
$\to S_{ABCD} = 2S_{ABD} = 2\cdot\dfrac{AB^2\sqrt3}{4} = \dfrac{a^2\sqrt3}{2}$
Do $AC = a\sqrt3 > BD = a$
$\to AC$ là đường chéo lớn của đáy $ABCD$
$\to BD’$ là đường chéo nhỏ của lăng trụ
$\to AC = BD’ = a\sqrt3$
Áp dụng định lý $Pythagoras$ ta được:
$BD’^2 = BD^2 + DD’^2$
$\to DD’ = \sqrt{BD’^2 -BD^2} = \sqrt{3a^2 + a^2} = a\sqrt2$
Do đó:
$V = S_{ABCD}.DD’ = \dfrac{a^2\sqrt3}{2}\cdot a\sqrt2= \dfrac{a^3\sqrt6}{2}$