Câu hỏi:
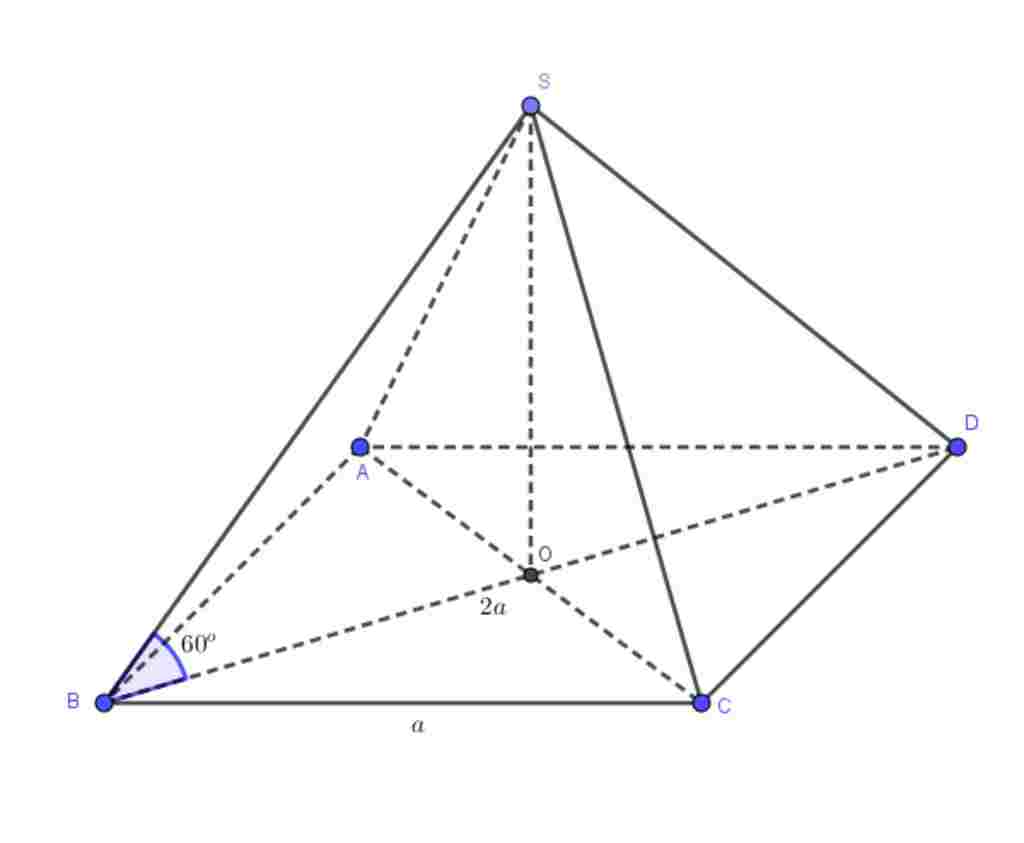
Giúp em bài tập về nhà Toán lớp 12 câu hỏi như sau: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AC=2a, BC=a. Đỉnh S cách đều 3 điểm A,B,C , SB tạo với đáy góc 60°. Tính thể tích hình chóp?
Trả lời 1:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
Giải đáp:
$V_{S.ABCD} =a^3$
Lời giải và giải thích chi tiết:
Ta có:
$S$ cách đều $A,B,C$
$\Rightarrow SA = SB = SC$
Gọi $O$ là hình chiếu của $S$ là $(ABCD)$
$\Rightarrow OA = OB = OC$
$\Rightarrow \left\{O\right\} = AC\cap BD$
$\Rightarrow OB = \dfrac{1}{2}AC = a$
Áp dụng định lý Pytago, ta được:
$AC^2 = AB^2 + BC^2$
$\Rightarrow AB = \sqrt{AC^2 – BC^2} = \sqrt{4a^2 – a^2} = a\sqrt3$
Mặt khác:
$SO\perp (ABCD)$
$\Rightarrow \widehat{(SB;(ABCD))} = \widehat{SBO} = 60^o$
$\Rightarrow SO = OB.\tan60^o = a\sqrt3$
Ta được:
$V_{S.ABCD} = \dfrac{1}{3}S_{ABCD}.SO = \dfrac{1}{3}AB.BC.SO = \dfrac{1}{3}.a\sqrt3.a.a\sqrt3 = a^3$