Câu hỏi:
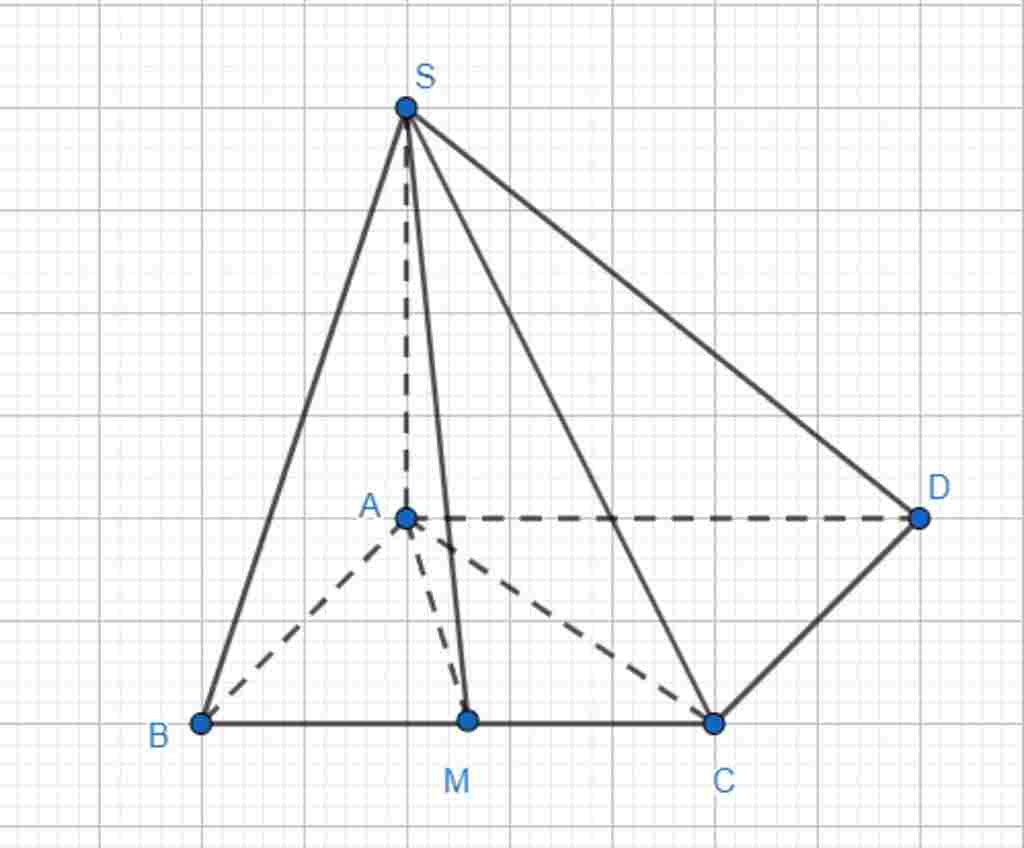
Giúp em bài tập về nhà Toán lớp 12 câu hỏi như sau: Cho hình chóp S.ABCD có đáy ABCD là hình thoi , góc BAD bằng 120 độ . AB = a. hai mặt phẳng SAB và SAD cùng vuông góc với đáy . Góc giữa SBC và mặt phẳng đáy là 60 độ . Tính thể tích V của chóp S.ABCD
Trả lời 2:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn: Mình giải trong hình 😀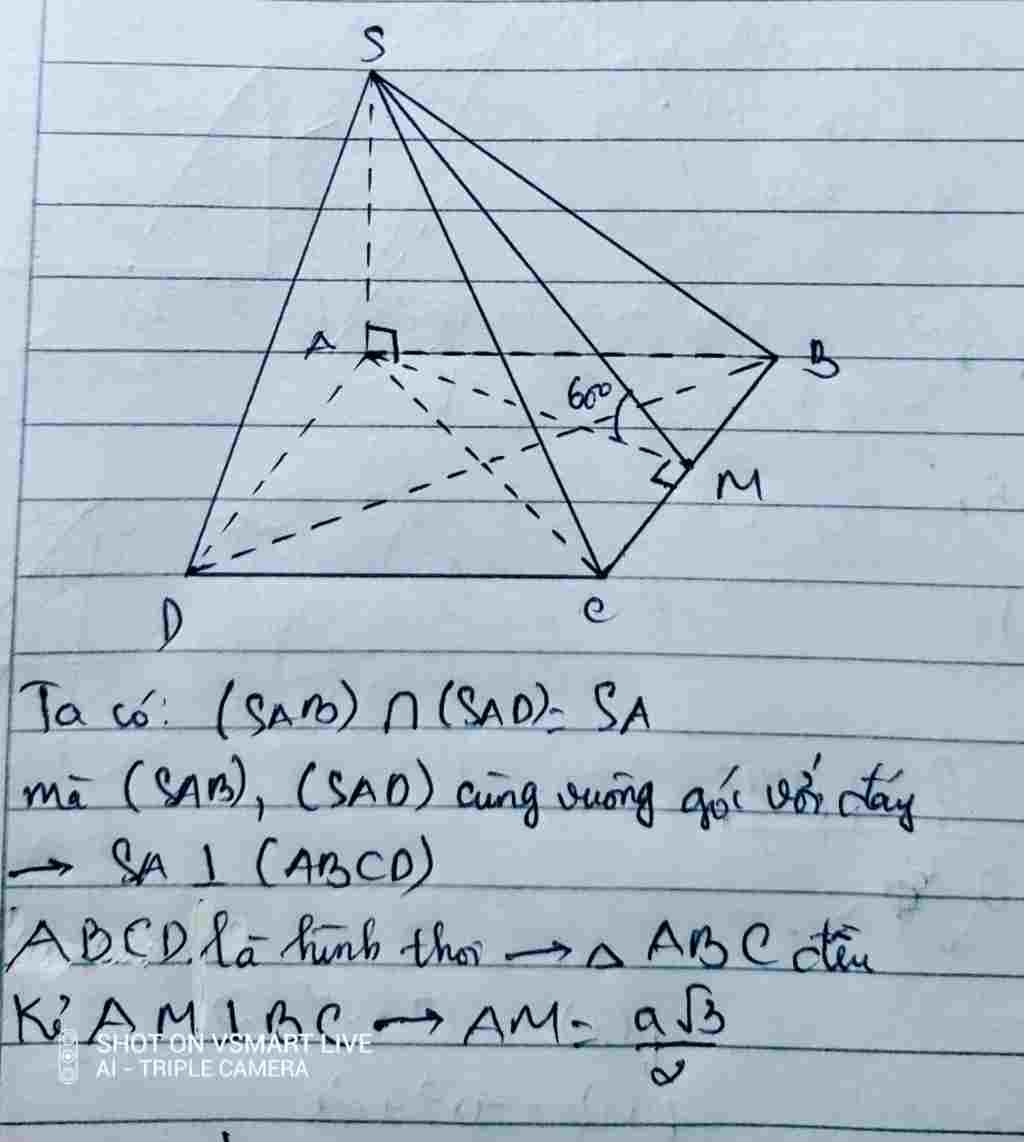
Trả lời 1:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
Giải đáp+ Lời giải và giải thích chi tiết:
Xét hình thoi $ABCD$ có $\widehat{BAD}=120^o$
$\Rightarrow \widehat{BAC}=60^o$
$\Rightarrow ΔABC$ đều
$\Rightarrow AM=\dfrac{a\sqrt{3}}{2}$
Do $ΔABC$ dề và $AM$ là trung tuyến nên $AM⊥BC$
Vì $(SAB)⊥(ABCD), (SAD)⊥(ABCD)$ và $(SAB)∩(SAD)=SA$ nên $SA⊥(ABCD)$
$\Rightarrow SA⊥BC$
$\Rightarrow BC⊥(SAM)$
$\Rightarrow (SBC)⊥(SAM)$
Mặt khác: $SA⊥(ABCD)$
$\Rightarrow (SAM)⊥(ABCD)$
$\Rightarrow \widehat{((SBC),(ABCD))}=\widehat{SMA}=60^o$
Xét $ΔSAM$ vuông tại $A$ có $SA=AM.\tan{\widehat{SMA}}= \dfrac{a\sqrt{3}}{2}.\tan{60^o}=\dfrac{3a}{2}$
Vậy $V_{S.ABCD}=\dfrac{1}{3}.SA.S_{ABCD}=\dfrac{1}{3}.\dfrac{3a}{2}.AB.AD.\sin{120^o}=\dfrac{1}{3}.\dfrac{3a}{2}.a.a.\sin{120^o}=\dfrac{a^3\sqrt{3}}{4}$