Câu hỏi:
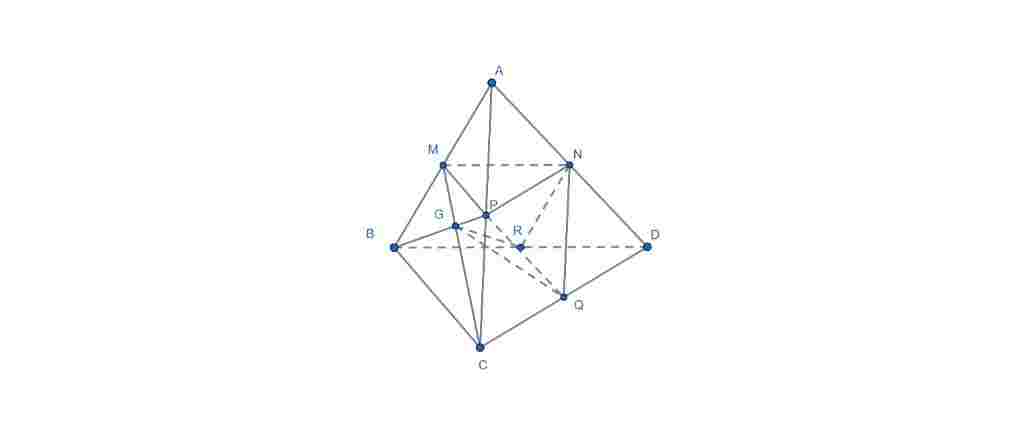
Giúp em bài tập về nhà Toán lớp 12 câu hỏi như sau: Cho tứ diện ABCD có thể tích là V. Gọi M, N, P, Q, R lần lượt là trung điểm các cạnh AB, AD, AC, DC, BD và G là trọng tâm tam giác ABC. Tính V khối đa diện lồi MNPQRG theo V
A.V/3
B.V/2
C.V/6
D.2V/5
Mọi người trình bày đầy đủ nhé nếu có thể thì vẽ hộ mình cái hình luôn ạ
Trả lời 2:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
Ta có thể tích của khối đa diện $MNPQRG$ là
$V_{MNPQRG} = V_{ABCD} – V_{AMNP} – V_{DNRQ} – V_{G.BCQR} – V_{G.BRM} – V_{G.CPQ}$
Áp dụng công thức tỉ lệ thể tích ta có
$V_{AMNP} = V_{ABCD} . \dfrac{AM}{AB} . \dfrac{AP}{AC} . \dfrac{AN}{AD} = V . \dfrac{1}{2^3} = \dfrac{V}{8}$
và
$V_{DNRQ} = V_{ABCD} . \dfrac{DN}{DA} . \dfrac{DQ}{DC} . \dfrac{DR}{DB} = V . \dfrac{1}{2^3} = \dfrac{V}{8}$
Gọi $AG \cap BC = S$.
Khi đó ta có $\dfrac{GS}{AS} = \dfrac{1}{3}$ suy ra
$d(G, BCD) = \dfrac{GS}{AS} . d(A, (BCD)) = \dfrac{1}{3} d(A, (BCD))$
Mặt khác, lại có tam giác $DRQ$ đồng dạng với tam giác $DBC$ với tỉ số $\dfrac{1}{2}$ suy ra
$S_{DRQ} = \dfrac{1}{4} S_{BCD}$
Vậy $S_{BCQR} = \dfrac{3}{4} S_{BCD}$
Ta có
$V_{G.BCQR} = \dfrac{1}{3} . S_{BCQR} . d(G, BCQR)$
$= \dfrac{1}{3} . \dfrac{3}{4} S_{BCD} . \dfrac{1}{3} d(A, (BCD))$
$= \dfrac{3}{4} . \dfrac{1}{3} . V = \dfrac{V}{4}$
Ta có tam giác $BRM$ đồng dạng với tam giác $BDA$ với tỉ số $\dfrac{1}{2}$, suy ra
$S_{BRM} = \dfrac{1}{4} S_{BDA}$
Mặt khác, lại có
$\dfrac{d(G, (BRM))}{d(C, (BDA))} = \dfrac{GM}{CM} = \dfrac{1}{3}$
$<-> d(G, (BRM)) = \dfrac{1}{3} d(C, (BDA))$
Ta có
$V_{G.BRM} = \dfrac{1}{3} . d(G, (BRM)) . S_{BRM}$
$= \dfrac{1}{3} . \dfrac{1}{3} d(C, (BDA)) . \dfrac{1}{4} S_{BDA}$
$= \dfrac{1}{3} . \dfrac{1}{4} V_{ABCD}$
$= \dfrac{V}{12}$
Tính toán tương tự ta cũng có
$V_{G.CPQ} = \dfrac{V}{12}$
Vậy suy ra
$V_{MNPQRG} = V – \dfrac{V}{8} – \dfrac{V}{8} – \dfrac{V}{4} – \dfrac{V}{12} – \dfrac{V}{12}= \dfrac{V}{3}$
Giải đáp $A$.
Trả lời 1:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
Giải đáp:
A. $\dfrac V 3$
Lời giải và giải thích chi tiết:
$V_{MNPQRG}=V_{G.MPQR}+V_{N.MPQR}$ ($V_{G.MPQR};V_{CMPQR}$ chung đáy MPQR, chiều cao hạ từ G và C có tỉ lệ bằng $\dfrac{GM}{CM}=\dfrac13$)
$=\dfrac13V_{C.MPQR}+V_{N.MPQR}$ (tứ giác PCQN là hình bình hành, nên C và N đối xứng nhau qua trung điểm PQ, nên hình chiếu hạ từ C và N lên MPQN là bằng nhau)
$=\dfrac43V_{N.MPQR}$ (tứ giác MPQN là hình bình hành nên $S_{MPR}=S_{QRP}$)
$=\dfrac43.2.V_{N.MPR}$
$=\dfrac83.V_{P.MNR}$
$=\dfrac83.\dfrac12.V_{C.MNR}$
$=\dfrac43.\dfrac14.V_{C.ABD}=\dfrac V3$