Câu hỏi:
Giúp em bài tập về nhà Toán lớp 12 câu hỏi như sau: Mọi người giúp mình với ạ
Cho khối chóp SABCD có đáy ABCD là hình vuông cạnh a, SA vuông (ABCD) và SA = a căn 2 Gọi M là trung điểm cạnh SC khoảng cách từ M đến mặt phẳng (SBD) bằng
Trả lời 2:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
Vote 5* nha
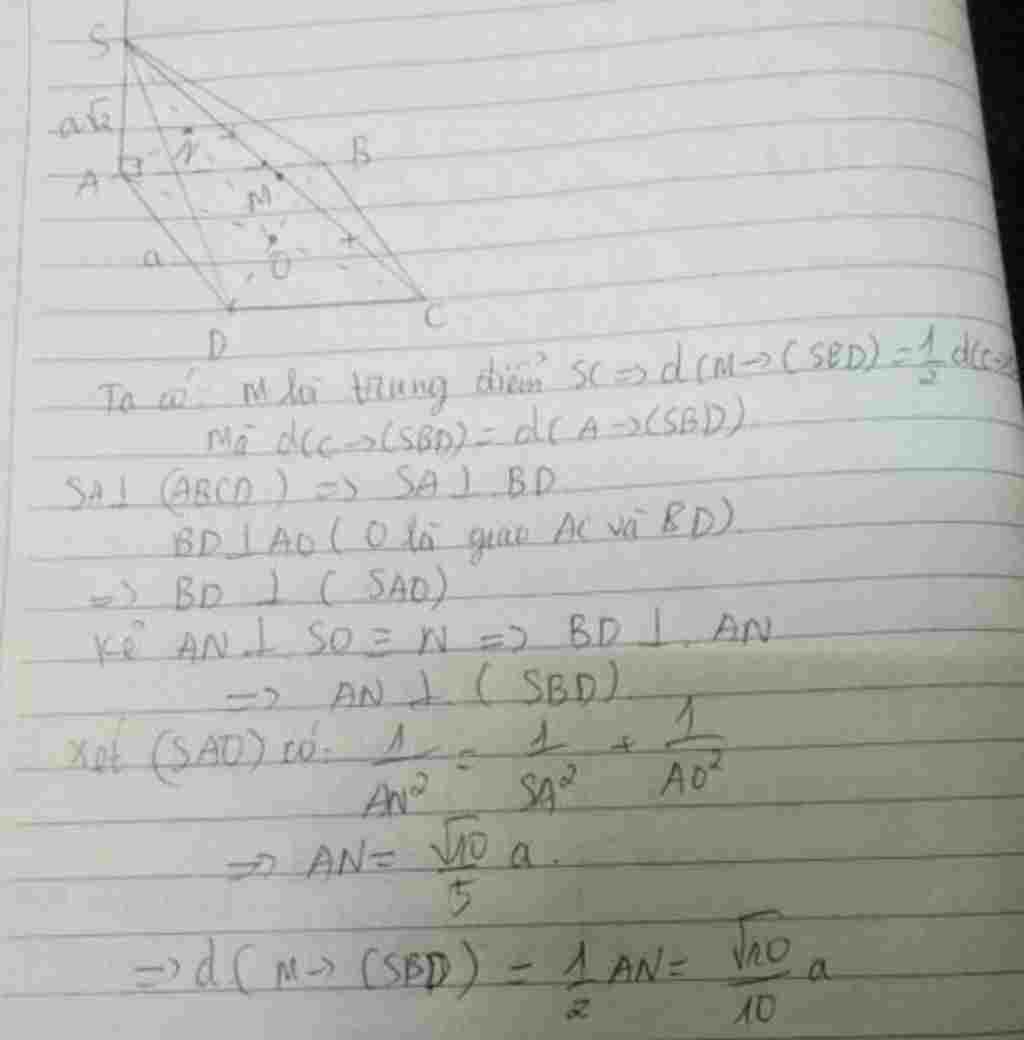
Trả lời 1:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
$d(M,(SBD))=\dfrac{1}{2}d(C,(SBD))=\dfrac{1}{2}d(A,(SBD))$
Gọi $O=AC∩BD$, kẻ $AH⊥SO$, ta có:
$BD⊥AC, BD⊥SA → BD⊥(SAC) → BD⊥AH$
Mà $AH⊥SO, SO⊂(SBD) → AH⊥(SBD)$ hay $d(A,(SBD))=AH$
Ta có:
$AH=\dfrac{SA.AO}{\sqrt[]{SA^2+AO^2}}$
$=\dfrac{a\sqrt[]{2}.\dfrac{a\sqrt[]{2}}{2}}{\sqrt[]{2a^2+\dfrac{a^2}{2}}}$
$=\dfrac{a\sqrt[]{10}}{5}$
Vậy khoảng cách từ $M$ đến $(SBD)$ bằng $\dfrac{a\sqrt[]{10}}{10}$.





