Câu hỏi:
Giúp em bài tập về nhà Toán lớp 12 câu hỏi như sau: Tìm tất cả các giá trị thực của m để hàm số y = x^3 – 3mx^2+(m-1)x+2 có cực đại, cực tiểu và các điểm cực trị của đồ thị hàm số có hoành độ dương
Trả lời 2:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
Mình trình bày chi tiết ở trong hình!
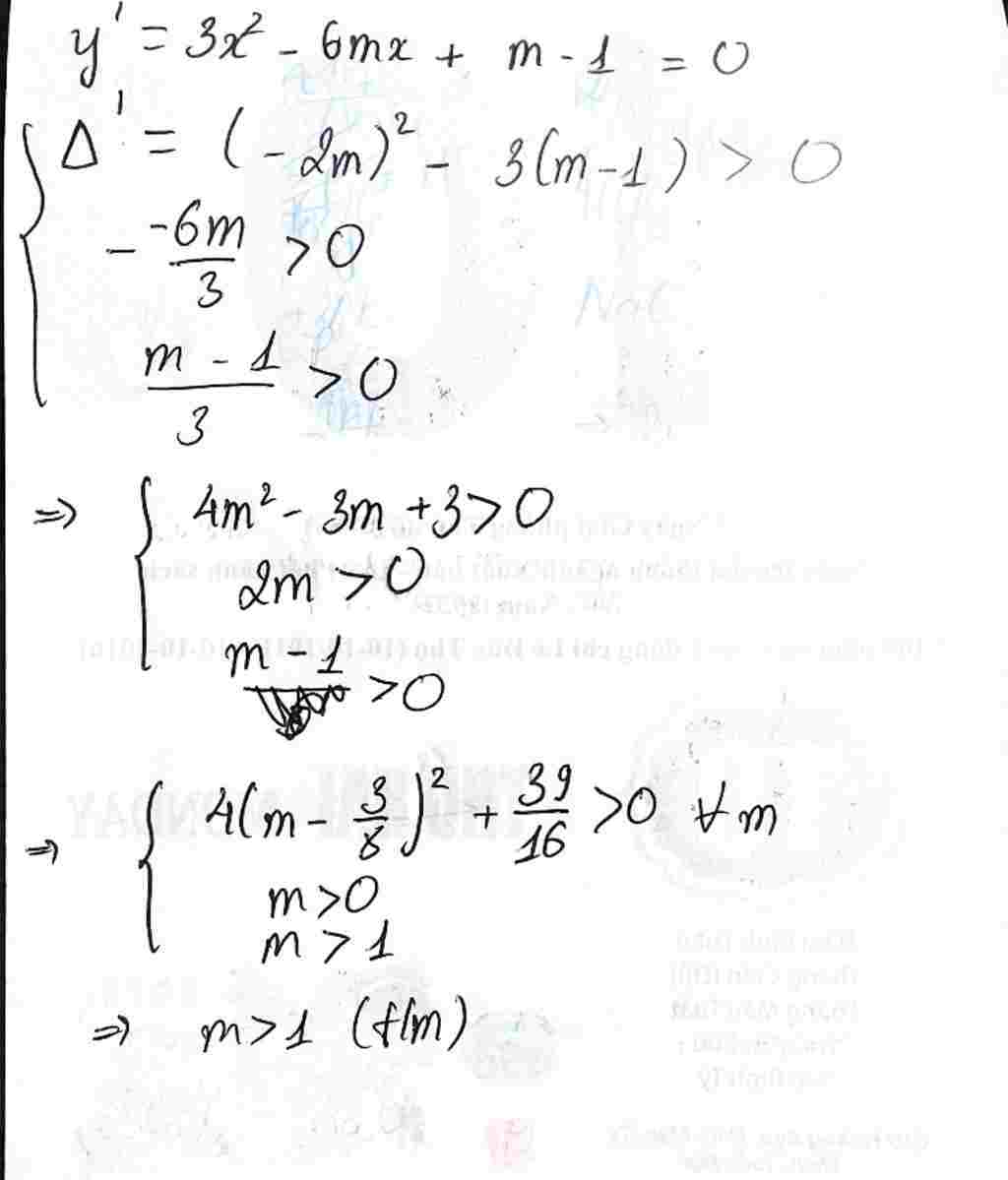
Trả lời 1:
Gia Sư Hoàng Khang gữi câu trả lời dành cho bạn:
Giải đáp: $m>1$
Lời giải và giải thích chi tiết:
Ta có:
$y’=3x^2-6mx+m-1$
$\to$Để hàm số có cực đại, cực tiểu và các điểm cực trị của đồ thị hàm số có hoành độ dương
$\to $Phương trình $3x^2-6mx+m-1=0$ có $2$ nghiệm dương phân biệt
$\to \begin{cases} \Delta’=(-2m)^2-3\cdot (m-1)>0\\ -\dfrac{-6m}{3}>0\\ \dfrac{m-1}{3}>0\end{cases}$
$\to \begin{cases} 4m^2-3m+3>0\\ 2m>0\\ m-1>0\end{cases}$
$\to \begin{cases} 4\left(m-\dfrac{3}{8}\right)^2+\dfrac{39}{16}>0\\ m>0\\ m>1\end{cases}$
$\to m>1$





